Hvordan bestemme posisjonen til kroppens tyngdepunkt. Bestemme koordinatene til tyngdepunktet til planfigurer

– beregne tyngdepunktet til en flat avgrenset figur. Mange lesere forstår intuitivt hva tyngdepunktet er, men jeg anbefaler likevel å gjenta materialet fra en av leksjonene analytisk geometri, hvor jeg fant ut problem om tyngdepunktet til en trekant og dechiffrerte den fysiske betydningen av dette begrepet i en tilgjengelig form.

I uavhengige og testoppgaver for løsningen foreslås som regel det enkleste tilfellet - en flat avgrenset homogen figur, det vil si en figur med konstant fysisk tetthet - glass, tre, tinn, støpejernsleker, vanskelig barndom, etc. Videre, som standard, vil vi bare snakke om slike tall =)

Den første regelen og enkleste eksempelet : hvis en flat figur har senter for symmetri, så er det tyngdepunktet til denne figuren. For eksempel midten av en rund homogen plate. Det er logisk og forståelig i hverdagen - massen til en slik figur er "ganske fordelt i alle retninger" i forhold til sentrum. Jeg vil ikke snu det.

Men i harde realiteter er det usannsynlig at de vil gi deg en søt elliptisk sjokoladeplate, så du må bevæpne deg med noen seriøse kjøkkenverktøy:

Koordinatene til tyngdepunktet til en flat homogen begrenset figur beregnes ved å bruke følgende formler:

, eller:

, hvor er området i regionen (figur); eller veldig kort:

, Hvor

Vi vil konvensjonelt kalle integralet "X"-integralet, og integralet for "Y"-integralet.

Hjelpemerknad : for flat begrenset heterogen figurer, hvis tetthet er spesifisert av funksjonen, formlene er mer komplekse:
, Hvor - massen til figuren;i tilfelle av jevn tetthet er de forenklet til formlene ovenfor.

Faktisk slutter all nyheten med formlene, resten er din ferdighet løse doble integraler Nå er det forresten en flott mulighet til å øve og forbedre teknikken din. Og som du vet, det er ingen grense for perfeksjon =)

La oss kaste inn en forfriskende porsjon parabler:

Eksempel 1

Finn koordinatene til tyngdepunktet til en homogen flat figur, begrenset av linjer.

Løsning: linjene her er elementære: den definerer x-aksen, og ligningen – en parabel, som enkelt og raskt kan konstrueres ved hjelp av geometriske transformasjoner av grafer:

– parabel, flyttet 2 enheter til venstre og 1 enhet ned.

Jeg vil fullføre hele tegningen på en gang med det ferdige punktet på figurens tyngdepunkt:

Regel to: hvis figuren har symmetriakse, så ligger tyngdepunktet til denne figuren nødvendigvis på denne aksen.

I vårt tilfelle er figuren symmetrisk mht rett, det vil si at vi allerede kjenner "x"-koordinaten til punktet "em".

Legg også merke til at vertikalt er tyngdepunktet forskjøvet nærmere x-aksen, siden figuren er mer massiv der.

Ja, kanskje ikke alle har helt forstått hva tyngdepunktet er: løft pekefingeren opp og plasser mentalt den skyggelagte "sålen" med en prikk på. Teoretisk sett bør tallet ikke falle.

Vi finner koordinatene til figurens tyngdepunkt ved hjelp av formlene , Hvor .

Rekkefølgen for å krysse området (figur) er åpenbar her:

Merk følgende! Bestemme den mest fordelaktige traverseringsrekkefølgen en gang- og bruke den for alle integraler!

1) Beregn først arealet av figuren. På grunn av den relative enkelheten til integralet, kan løsningen skrives kompakt, det viktigste er å ikke bli forvirret i beregningene:

Vi ser på tegningen og anslår arealet ved celler. Det viste seg å handle om saken.

2) X-koordinaten til tyngdepunktet er allerede funnet ved "grafisk metode", så du kan referere til symmetri og gå videre til neste punkt. Imidlertid anbefaler jeg fortsatt ikke å gjøre dette - det er stor sannsynlighet for at løsningen vil bli avvist med ordlyden "bruk formelen."

Vær oppmerksom på at her kan du utelukkende klare deg med hoderegning – noen ganger er det slett ikke nødvendig å redusere brøker til en fellesnevner eller plage kalkulatoren.

Dermed:
, som er det som kreves for å få tak i.

3) Finn ordinaten til tyngdepunktet. La oss beregne "spill"-integralen:

Men her ville det vært vanskelig uten en kalkulator. Bare i tilfelle, vil jeg kommentere at som et resultat av å multiplisere polynomer, får vi 9 ledd, og noen av dem er like. Jeg ga lignende vilkår muntlig (som vanligvis gjøres i lignende tilfeller) og skrev umiddelbart ned totalbeløpet.

Som et resultat:
, som er veldig, veldig lik sannheten.

På sluttfasen markerer du et punkt på tegningen. I følge vilkåret var det ikke krav om å tegne noe, men i de fleste oppgaver er vi tvunget til å tegne en figur. Men det er et absolutt pluss - en visuell og ganske effektiv verifisering av resultatet.

Svar:

De følgende to eksemplene er for deg å løse på egen hånd.

Eksempel 2

Finn koordinatene til tyngdepunktet til en homogen flat figur avgrenset av linjer

Forresten, hvis du forestiller deg hvordan parablen er plassert og ser punktene der den krysser aksen, så kan du faktisk klare deg uten tegning her.

Og mer komplisert:

Eksempel 3

Finn tyngdepunktet til en homogen flat figur avgrenset av linjer

Hvis du har problemer med å lage grafer, studer (gjenta) leksjon om parabler og/eller eksempel nr. 11 i artikkelen Doble integraler for dummies.

Eksempel på løsninger på slutten av leksjonen.

I tillegg finnes et titalls eller to lignende eksempler i det tilsvarende arkivet på siden Ferdige løsninger for høyere matematikk.

Vel, jeg kan ikke annet enn å glede fans av høyere matematikk, som ofte ber meg analysere vanskelige problemer:

Eksempel 4

Finn tyngdepunktet til en homogen flat figur avgrenset av linjer. Tegn figuren og dens tyngdepunkt på tegningen.

Løsning: tilstanden til denne oppgaven krever allerede kategorisk fullføring av tegningen. Men kravet er ikke så formelt! – selv en person med et gjennomsnittlig treningsnivå kan forestille seg denne figuren i tankene hans:

En rett linje kutter en sirkel i 2 deler, og en ekstra klausul (cm. lineære ulikheter) indikerer at vi snakker om et lite skyggelagt stykke.

Figuren er symmetrisk i forhold til en rett linje (avbildet med en stiplet linje), så tyngdepunktet skal ligge på denne linjen. Og åpenbart er koordinatene like modulo. En utmerket retningslinje som praktisk talt eliminerer muligheten for et feilsvar!

Nå dårlige nyheter=) I horisonten ruver en ubehagelig integral av roten, som vi undersøkte i detalj i eksempel nr. 4 i leksjonen Effektive metoder for å løse integraler. Og hvem vet hva annet vil bli trukket dit. Det ser ut til at på grunn av tilstedeværelsen sirkel lønnsomt, men ikke alt er så enkelt. Linjens ligning transformeres til formen og integralene vil heller ikke vise seg å være sukker (selv om fans trigonometriske integraler vil sette pris på). I denne forbindelse er det mer fornuftig å fokusere på kartesiske koordinater.

Rekkefølgen for å krysse figuren:

1) Regn ut arealet av figuren:

Det er mer rasjonelt å ta den første integralen subsumerer differensialtegnet:

Og i den andre integralen gjør vi standarderstatningen:

La oss beregne de nye grensene for integrasjon:

2) La oss finne .

Her i 2. integral ble det igjen brukt metode for å subsumere en funksjon under differensialtegnet. Øv og adopter disse optimalt (etter min mening) teknikker for å løse standard integraler.

Etter vanskelige og tidkrevende beregninger vender vi igjen oppmerksomheten mot tegningen (husk at poeng vi vet ikke ennå! ) og vi får dyp moralsk tilfredsstillelse fra den funnet verdi.

3) Basert på analysen utført tidligere, gjenstår det å forsikre seg om at .

Flott:

La oss trekke et poeng på tegningen. I henhold til vilkårets ordlyd skriver vi den ned som endelig svar:

En lignende oppgave for deg å løse på egen hånd:

Eksempel 5

Finn tyngdepunktet til en homogen flat figur avgrenset av linjer. Utfør tegningen.

Dette problemet er av interesse fordi det inneholder en figur av ganske liten størrelse, og hvis du gjør en feil et sted, er det stor sannsynlighet for at du "ikke kommer inn i" området i det hele tatt. Noe som absolutt er bra med tanke på beslutningskontroll.

Et eksempeldesign på slutten av leksjonen.

Noen ganger gir det mening overgang til polare koordinater i doble integraler. Det kommer an på figuren. Jeg søkte og søkte selv godt eksempel, men jeg fant det ikke, så jeg vil demonstrere løsningen ved å bruke det første demoproblemet i leksjonen ovenfor:


La meg minne deg på at i det eksemplet vi gikk til polare koordinater, fant ut rekkefølgen på å krysse området og beregnet arealet

La oss finne tyngdepunktet til denne figuren. Opplegget er det samme: . Verdien ses direkte fra tegningen, og "x"-koordinaten bør flyttes litt nærmere ordinataksen, siden den mer massive delen av halvsirkelen er plassert der.

I integraler bruker vi standard overgangsformler:

Sannsynligvis, mest sannsynlig, tok de ikke feil.

Forelesning 4. Tyngdepunkt.

Dette foredraget dekker følgende problemstillinger

1. Tyngdepunkt for et fast legeme.

2. Koordinater til tyngdepunktene til inhomogene legemer.

3. Koordinater til tyngdepunktene til homogene legemer.

4. Metoder for å bestemme koordinatene til tyngdepunktene.

5. Tyngdepunkt for noen homogene kropper.

Studiet av disse spørsmålene er nødvendig i fremtiden for å studere dynamikken i bevegelsen av kropper under hensyntagen til glidende friksjon og rullende friksjon, dynamikken i bevegelsen til massesenteret mekanisk system, kinetiske øyeblikk, for å løse problemer i disiplinen "Strength of Materials".

Bringer parallelle krefter.

Etter at vi har vurdert å bringe et flatt system og et vilkårlig romlig kraftsystem til sentrum, går vi igjen tilbake til å vurdere det spesielle tilfellet med et system med parallelle krefter.

Bringer to parallelle krefter.

I løpet av vurderingen av et slikt styrkesystem er følgende tre tilfeller av reduksjon mulig.

1. System med to kollineære krefter. La oss se på et system med to parallelle krefter rettet i én retning P Og Q, brukt på punkter EN Og I. Vi vil anta at kreftene er vinkelrett på dette segmentet (fig. 1, EN).

MED, som tilhører segmentet AB og oppfyller betingelsen:

AC/NE = Q/P.(1)

Hovedvektor av systemet R C = P + Q er lik i modul med summen av disse kreftene: R C = P + Q.

MED tatt i betraktning (1) er lik null:MC = P ∙ AC- Q∙ NE = 0.

Dermed fikk vi som et resultat av castingen: R C ≠ 0, MC= 0. Dette betyr at hovedvektoren er ekvivalent med resultanten som går gjennom reduksjonssenteret, det vil si:

Resultanten av kollineære krefter er lik i modul til summen, og dens virkelinje deler segmentet som forbinder punktene for deres påføring, i omvendt proporsjon med modulene til disse kreftene på en intern måte.

Merk at posisjonen til punktet MED vil ikke endres hvis kreftene R Og Q snu en vinkelα. Punktum MED, som har denne egenskapen kalles sentrum av parallelle krefter.

2. System av to antikollineær og krefter som ikke er like store. Måtte styrke P Og Q, brukt på punkter EN Og I, parallell, rettet i motsatte retninger og ulik i størrelse (fig. 1, b).

La oss velge et punkt som reduksjonssenter MED, som fortsatt tilfredsstiller relasjon (1) og ligger på samme linje, men utenfor segmentet AB.

Hovedvektoren til dette systemet R C = P + Q modulen vil nå være lik forskjellen mellom modulene til vektorene: R C = Q - P.

Hovedpoenget angående sentrum MED er fortsatt null:MC = P ∙ AC- Q∙ NE= 0, altså

Resulterende antikollineær og krefter som ikke er like store er lik forskjellen deres, rettet mot den større kraften, og dens virkelinje deler segmentet som forbinder punktene for deres påføring, i omvendt proporsjon med de ytre modulene til disse kreftene.

Figur 1

3. System av to antikollineær og krefter like store. La oss ta det forrige tilfellet med reduksjon som det første. La oss fikse kraften R, og styrke Q la oss rette modulen til kraften R.

Så kl Q → R i formel (1) forholdet AC/NE → 1. Dette betyr at AC → NE, altså avstanden AC →∞ .

I dette tilfellet modulen til hovedvektoren R C → 0, og modulen til hovedmomentet avhenger ikke av posisjonen til reduksjonssenteret og forblir lik den opprinnelige verdien:

MC = P ∙ AC- Q∙ NE = P ∙ ( AC- NE) =P ∙ ENB.

Så, i grensen har vi fått et system av krefter som R C = 0, MC≠ 0, og reduksjonssenteret fjernes til uendelig, som ikke kan erstattes av resultanten. Det er ikke vanskelig å gjenkjenne et par krefter i dette systemet, altså et par krefter har ingen resultat.

Sentrum av systemet med parallelle krefter.

Vurder systemet n styrke P i, brukt på punkterA i (x i , y jeg , z i) og parallelt med aksenOv med ort l(Fig. 2).

Hvis vi på forhånd utelukker tilfellet med et system som tilsvarer et par krefter, er det ikke vanskelig, basert på forrige avsnitt, å bevise eksistensen av dets resulterendeR.

La oss bestemme koordinatene til sentrumC(x c, y c, z c) parallelle krefter, det vil si koordinatene til påføringspunktet til resultanten av dette systemet.

Til dette formål bruker vi Varignons teorem, basert på hvilken:

M0 (R) = Σ M0(P i).

Fig.2

Vektormomentet til en kraft kan representeres som et vektorprodukt, derfor:

M 0 (R) = r c× R = Σ M0i(P i) = Σ ( r jeg× P i ).

Vurderer R = Rv ∙ l, A P i = Pvi ∙ l og bruke egenskapene vektor produkt, vi får:

r c × Rv ∙ l = Σ ( r jeg × Pvi ∙ l),

r c ∙ R v× l = Σ ( r jeg ∙ Pvi × l) = Σ ( r jeg ∙ Pvi ) × l,

eller:

[ r c R v - Σ ( r jeg Pvi )] × l= 0.

Det siste uttrykket er kun gyldig hvis uttrykket i hakeparenteser er lik null. Derfor utelater indeksenvog tar i betraktning at den resulterendeR = Σ P i , herfra får vi:

r c = (Σ P i r jeg )/(Σ P i ).

Projiserer den siste vektorlikheten på koordinataksen, får vi den nødvendige uttrykk for koordinatene til sentrum av parallelle krefter:

x c = (Σ P i x i)/(Σ P i );

y c = (Σ P i y jeg )/(Σ P i );(2)

z c = (Σ P i z i )/(Σ P i ).

Tyngdepunkt for kropper.

Koordinater til tyngdepunktene til en homogen kropp.

La oss vurdere fast vekt P og volum V i koordinatsystemet Oxyz, hvor er aksene x Og y koblet til jordens overflate, og aksen z rettet mot senit.

Hvis vi bryter kroppen i elementære deler med et volum∆ V Jeg , så vil tiltrekningskraften virke på hver del av den∆ P i, rettet mot jordens sentrum. La oss anta at kroppens dimensjoner er betydelig mindre enn jordens dimensjoner, da kan systemet av krefter som påføres de elementære delene av kroppen betraktes som ikke konvergerende, men parallell (fig. 3), og alle konklusjonene i forrige kapittel gjelder for det.

Fig.3

Definisjon . Tyngdepunktet til et fast legeme er sentrum for parallelle tyngdekrefter til de elementære delene av denne kroppen.

La oss minne deg på det egenvekt av en elementær del av kroppen kalles forholdet mellom dens vekt∆ P i til volum ∆ V Jeg : γ Jeg = ∆ P i/ ∆ V Jeg . For en homogen kropp er denne verdien konstant:γ Jeg = γ = P/ V.

Bytter ∆ inn i (2) P i = γ Jeg ∙∆ V Jeg i stedet for P i, tar hensyn til den siste bemerkningen og reduserer telleren og nevneren medg, vi får uttrykk for koordinatene til tyngdepunktet til en homogen kropp:

x c = (Σ ∆ V i∙ x i)/(Σ ∆ V i);

y c = (Σ ∆ V i∙ y jeg )/(Σ ∆ V i);(3)

z c = (Σ ∆ V i∙ z i )/(Σ ∆ V i).

Flere teoremer er nyttige for å bestemme tyngdepunktet.

1) Hvis et homogent legeme har et symmetriplan, er tyngdepunktet i dette planet.

Hvis aksene X Og på plassert i dette symmetriplanet, deretter for hvert punkt med koordinater. Og koordinaten i henhold til (3), vil være lik null, fordi totalt Alle medlemmer med motsatte fortegn blir ødelagt i par. Dette betyr at tyngdepunktet er lokalisert i symmetriplanet.

2) Hvis et homogent legeme har en symmetriakse, er kroppens tyngdepunkt på denne aksen.

Faktisk, i dette tilfellet, hvis aksenztegne langs symmetriaksen, for hvert punkt med koordinaterdu kan finne et punkt med koordinater og koordinater og , beregnet ved hjelp av formler (3), vil være lik null.

Det tredje teoremet er bevist på lignende måte.

3) Hvis en homogen kropp har et symmetrisenter, er tyngdepunktet til kroppen på dette punktet.

Og noen flere kommentarer.

Først. Hvis kroppen kan deles inn i deler der vekten og posisjonen til tyngdepunktet er kjent, er det ikke nødvendig å vurdere hvert punkt, og i formler (3) P i – bestemt som vekten av den tilsvarende delen og– som koordinatene til dets tyngdepunkt.

Sekund. Hvis kroppen er homogen, så vekten av en individuell del av den, Hvor - egenvekt materialet som kroppen er laget av, og V i - volumet til denne delen av kroppen. Og formler (3) vil ha en mer praktisk form. For eksempel,

Og på samme måte, hvor - volum av hele kroppen.

Tredje note. La kroppen ha form som en tynn plate med et område F og tykkelse t, liggende i flyet Oksy. Erstatter i (3)∆ V Jeg =t ∙ ∆F Jeg , vi får koordinatene til tyngdepunktet til en homogen plate:

x c = (Σ ∆ F i∙ x i) / (Σ ∆ F i);

y c = (Σ ∆ F i∙ y jeg ) / (Σ ∆ F i).

z c = (Σ ∆ F i∙ z Jeg ) / (Σ ∆ F i).

Hvor - koordinater for tyngdepunktet til individuelle plater;– total kroppsareal.

Fjerde note. For en kropp i form av en tynn buet stang av lengde L med tverrsnittsareal en elementært volum∆ V Jeg = en ∙∆ L Jeg , Derfor koordinater for tyngdepunktet til en tynn buet stang vil være lik:

x c = (Σ ∆ L i∙ x i)/(Σ ∆ L i);

y c = (Σ ∆ L i∙ y jeg )/(Σ ∆ L i);(4)

z c = (Σ ∆ L i∙ z i )/(Σ ∆ L i).

Hvor – koordinater til tyngdepunktetJeg-th seksjon; .

Merk at tyngdepunktet ifølge definisjonen er et geometrisk punkt; den kan også ligge utenfor grensene til en gitt kropp (for eksempel for en ring).

Merk.

I denne delen av kurset skiller vi ikke mellom tyngdekraft, tyngdekraft og kroppsvekt. I virkeligheten er tyngdekraften forskjellen mellom jordens gravitasjonskraft og sentrifugalkraften forårsaket av rotasjonen.

Koordinater til tyngdepunktene til inhomogene legemer.

Tyngdepunktkoordinater inhomogent fast stoff(Fig.4) i det valgte referansesystemet bestemmes som følger:

Fig.4

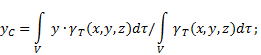
Hvor - vekt per volumenhet av en kropp (spesifikk vekt)

- hele kroppsvekten.

ujevn overflate(fig. 5), så bestemmes koordinatene til tyngdepunktet i det valgte referansesystemet som følger:

Fig.5

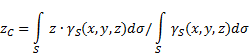
Hvor - vekt per enhet kroppsareal,

- hele kroppsvekten.

Hvis det faste er ujevn linje(fig. 6), så bestemmes koordinatene til tyngdepunktet i det valgte referansesystemet som følger:

Fig.6

Hvor - vekt per kroppslengde,

Hele kroppsvekten.

Metoder for å bestemme koordinatene til tyngdepunktet.

Basert på de generelle formlene oppnådd ovenfor, er det mulig å indikere spesifikke metoder bestemme koordinatene til legemers tyngdepunkt.

1. Symmetri. Hvis et homogent legeme har et plan, akse eller symmetrisenter (fig. 7), så ligger dets tyngdepunkt henholdsvis i symmetriplanet, symmetriaksen eller i symmetrisenteret.

Fig.7

2. Splitting. Kroppen er delt inn i et begrenset antall deler (fig. 8), for hver av disse er posisjonen til tyngdepunktet og området kjent.

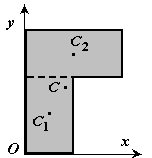
Fig.8

S =S1 +S2.

3.Negativt arealmetode. Et spesielt tilfelle av partisjoneringsmetoden (fig. 9). Det gjelder kropper som har utskjæringer dersom tyngdepunktene til kroppen uten utskjæringen og utskjæringsdelen er kjent. En kropp i form av en plate med en utskjæring er representert ved en kombinasjon av en solid plate (uten utskjæring) med et område S 1 og området til den kuttede delen S2.

Fig.9

S = S 1 - S 2.

4.Grupperingsmetode. Det er et godt supplement til de to siste metodene. Etter å ha delt en figur inn i dens komponentelementer, er det praktisk å kombinere noen av dem igjen for deretter å forenkle løsningen ved å ta hensyn til symmetrien til denne gruppen.

Tyngdepunktene til noen homogene kropper.

1) Tyngdepunktet til en sirkelbue. Tenk på buen AB radiusR med midtvinkel. På grunn av symmetri ligger tyngdepunktet til denne buen på aksenOkse(Fig. 10).

Fig.10

La oss finne koordinaten i henhold til formelen . For å gjøre dette, velg på buen AB element MM ’ lengde, hvis posisjon bestemmes av vinkelen. Koordinere X element MM' vil. Erstatter disse verdiene X Og d l og med tanke på at integralet må strekkes over hele lengden av buen, får vi:

der L er lengden av buen AB, lik .

Herfra finner vi til slutt at tyngdepunktet til en sirkelbue ligger på dens symmetriakse i avstand fra sentrum O lik

hvor er vinkelen målt i radianer.

2) Tyngdepunkt for trekantens område. Tenk på en trekant som ligger i flyet Oksy, koordinatene til toppunktene som er kjent: A i (x i,y jeg ), (Jeg= 1,2,3). Bryt trekanten i smale strimler parallelt med siden EN 1 EN 2, kommer vi til at trekantens tyngdepunkt må tilhøre medianen EN 3 M 3 (fig. 11).

Fig.11

Bryte en trekant i strimler parallelt med siden EN 2 EN 3, kan vi verifisere at den må ligge på medianen EN 1 M 1 . Dermed, tyngdepunktet til en trekant ligger i skjæringspunktet mellom medianene, som, som kjent, skiller en tredje del fra hver median, regnet fra den tilsvarende siden.

Spesielt for medianen EN 1 M 1 får vi, tar hensyn til at koordinatene til punktet M 1 - dette er det aritmetiske gjennomsnittet av koordinatene til toppunktene EN 2 og EN 3 :

x c = x 1 + (2/3) ∙ (xM 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.

Dermed er koordinatene til trekantens tyngdepunkt det aritmetiske gjennomsnittet av koordinatene til hjørnene:

x c =(1/3) Σ x i ; y c =(1/3) Σ y jeg .

3) Tyngdepunkt for området til en sirkulær sektor. Betrakt en sektor av en sirkel med radius R med midtvinkel 2α , plassert symmetrisk om aksen Okse (Fig. 12).

Det er åpenbart det y c = 0, og avstanden fra sentrum av sirkelen som denne sektoren er kuttet fra til tyngdepunktet kan bestemmes av formelen:

Fig.12

Den enkleste måten å beregne dette integralet på er ved å dele integrasjonsdomenet i elementære sektorer med en vinkel dφ . Nøyaktig til infinitesimals av første orden, en slik sektor kan erstattes av en trekant med en base lik R × dφ og høyde R. Arealet til en slik trekant dF =(1/2)R 2 ∙ dφ , og tyngdepunktet er i en avstand på 2/3 R fra toppunktet, derfor setter vi i (5). x = (2/3)R∙ cosφ. Erstatter i (5) F= α R 2, får vi:

Ved å bruke den siste formelen beregner vi spesielt avstanden til tyngdepunktet halvsirkel.

Ved å erstatte α = π /2 i (2), får vi: x c = (4 R)/(3π) ≅ 0,4 R .

Eksempel 1.La oss bestemme tyngdepunktet til den homogene kroppen vist i fig. 1. 3.

Fig.13

Løsning.Kroppen er homogen, bestående av to deler med en symmetrisk form. Koordinater for deres tyngdepunkt:

Volumene deres:

Derfor er koordinatene til kroppens tyngdepunkt

Eksempel 2. La oss finne tyngdepunktet til en plate bøyd i rett vinkel. Mål er på tegningen (fig. 14).

Fig.14

Løsning. Koordinater til tyngdepunktene:

0.

Områder:

Derfor:

Eksempel 3. På et firkantet ark cm firkantet hull kuttet cm (fig. 15). La oss finne tyngdepunktet til arket. Eksempel 4. Finn posisjonen til tyngdepunktet til platen vist i fig. 16. Mål er oppgitt i centimeter.

Fig.16

Løsning. La oss dele platen inn i figurer (fig. 17), sentre hvor alvorlighetsgraden er kjent.

Arealene til disse figurene og koordinatene til deres tyngdepunkt:

1) et rektangel med sidene 30 og 40 cm,S 1 =30 ∙ 40=1200 cm 2 ; x 1=15 cm; på 1 = 20 cm.

2) høyre trekant med en base på 50 cm og en høyde på 40 cm;S 2 =0,5 ∙ 50 ∙ 40 = 1000 cm 2 ; X 2 =30+50/3=46,7 cm; y 2 =40/3 =13,3 cm;

3) halv sirkel radius sirkel r = 20 cm;S 3 =0,5 ∙π∙ 202 =628 cm 2 ; X 3 =4 R /3 π =8,5 cm; på

Løsning. Husk at i fysikk tettheten til en kroppρ og dens egenvektgrelatert av relasjonen:γ = ρ g , Hvorg - tyngdeakselerasjon. For å finne massen til en slik homogen kropp, må du multiplisere tettheten med volumet.

Fig.19

Begrepet "lineær" eller "lineær" tetthet betyr at for å bestemme massen til en fagverksstang, må den lineære tettheten multipliseres med lengden på denne stangen.

For å løse problemet kan du bruke partisjoneringsmetoden. Ved å representere en gitt fagverk som en sum av 6 individuelle stenger, får vi:

HvorL i lengdeJeg fagverksstang, ogx i , y jeg - koordinatene til tyngdepunktet.

Løsningen på dette problemet kan forenkles ved å gruppere de siste 5 stolpene på fagverket. Det er lett å se at de danner en figur med et symmetrisenter plassert i midten av den fjerde stangen, der tyngdepunktet til denne gruppen av staver er plassert.

Dermed kan et gitt fagverk representeres av en kombinasjon av bare to grupper av stenger.

Den første gruppen består av den første stangen, for denL 1 = 4 m,x 1 = 0 m,y 1 = 2 m Den andre gruppen av stenger består av fem stenger, for denL 2 = 20 m,x 2 = 3 m,y 2 = 2 m.

Koordinatene til tyngdepunktet til fagverket er funnet ved å bruke formelen:

x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 m;

y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 m.

Merk at sentrum MED ligger på den rette linjen som forbinder MED 1 og MED 2 og deler segmentet MED 1 MED 2 angående: MED 1 MED/SS 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.

Selvtest spørsmål

– Hva kalles sentrum av parallelle krefter?

- Hvordan bestemmes koordinatene til sentrum av parallelle krefter?

- Hvordan bestemme sentrum av parallelle krefter hvis resultant er null?

- Hvilke egenskaper har sentrum av parallelle krefter?

- Hvilke formler brukes for å beregne koordinatene til sentrum av parallelle krefter?

– Hva kalles tyngdepunktet til en kropp?

– Hvorfor kan gravitasjonskreftene til jorden som virker på et punkt på en kropp tas som et system av parallelle krefter?

- Skriv ned formelen for å bestemme posisjonen til tyngdepunktet til inhomogene og homogene legemer, formelen for å bestemme posisjonen til tyngdepunktet til flate seksjoner?

- Skriv ned formelen for å bestemme posisjonen til tyngdepunktet til enkel geometriske former: rektangel, trekant, trapes og halvsirkel?

– Hva kalles det statiske arealmomentet?

- Gi et eksempel på en kropp hvis tyngdepunkt er plassert utenfor kroppen.

- Hvordan brukes egenskapene til symmetri for å bestemme tyngdepunktene til legemer?

- Hva er essensen av metoden med negative vekter?

- Hvor ligger tyngdepunktet til en sirkelbue?

- Hvilken grafisk konstruksjon kan brukes for å finne tyngdepunktet til en trekant?

- Skriv ned formelen som bestemmer tyngdepunktet til en sirkulær sektor.

- Ved å bruke formler som bestemmer tyngdepunktene til en trekant og en sirkulær sektor, utlede en lignende formel for et sirkulært segment.

- Hvilke formler brukes for å beregne koordinatene til tyngdepunktene til homogene kropper, flate figurer og linjer?

- Hva kalles det statiske momentet til arealet til en plan figur i forhold til aksen, hvordan beregnes det og hvilken dimensjon har det?

- Hvordan bestemme posisjonen til tyngdepunktet til et område hvis posisjonen til tyngdepunktene til dets individuelle deler er kjent?

- Hvilke hjelpesetninger brukes for å bestemme posisjonen til tyngdepunktet?

Rektangel. Siden et rektangel har to symmetriakser, er dets tyngdepunkt i skjæringspunktet mellom symmetriaksene, dvs. i skjæringspunktet mellom diagonalene til rektangelet.

Triangel. Tyngdepunktet ligger i skjæringspunktet mellom medianene. Fra geometri er det kjent at medianene til en trekant skjærer hverandre i ett punkt og er delt i forholdet 1:2 fra basen.

Sirkel. Siden en sirkel har to symmetriakser, er dens tyngdepunkt i skjæringspunktet mellom symmetriaksene.

Halvsirkel. En halvsirkel har én symmetriakse, så ligger tyngdepunktet på denne aksen. En annen koordinat for tyngdepunktet beregnes med formelen: .

Mange strukturelle elementer er laget av standard rullede produkter - vinkler, I-bjelker, kanaler og andre. Alle dimensjoner, så vel som geometriske egenskaper til rullede profiler, er tabelldata som kan finnes i referanselitteratur i tabeller med normalt sortiment (GOST 8239-89, GOST 8240-89).

Eksempel 1. Bestem posisjonen til tyngdepunktet til figuren vist på figuren.

Løsning:

Vi velger koordinataksene slik at okseaksen går langs den laveste Generell størrelse, og Oy-aksen er langs den generelle dimensjonen lengst til venstre.

Vi bryter en kompleks figur inn minimal mengde enkle figurer:

rektangel 20x10;

trekant 15x10;

sirkel R=3 cm.

Vi beregner arealet til hver enkel figur og dens koordinater til tyngdepunktet. Beregningsresultatene legges inn i tabellen

Figur nr.	Området til figur A,	Tyngdepunktkoordinater

Svar: C(14,5; 4,5)

Eksempel 2 . Bestem koordinatene til tyngdepunktet til en sammensatt seksjon som består av et ark og rullede seksjoner.

Løsning.

Vi velger koordinataksene som vist på figuren.

La oss angi tallene med tall og skrive ut de nødvendige dataene fra tabellen:

Figur nr.	Området til figur A,	Tyngdepunktkoordinater

Vi beregner koordinatene til figurens tyngdepunkt ved å bruke formlene:

Svar: C(0; 10)

Laboratoriearbeid nr. 1 "Bestemmelse av tyngdepunktet til sammensatte flate figurer"

Mål: Bestem tyngdepunktet til en gitt flat kompleks figur ved hjelp av eksperimentelle og analytiske metoder og sammenlign resultatene deres.

Arbeidsordre

Tegn den flate figuren i notatbøkene i størrelse, og angi koordinataksene.

Bestem tyngdepunktet analytisk.

1. Del figuren inn i minimum antall figurer hvis tyngdepunkt vi vet hvordan vi skal bestemme.

   Angi arealene og koordinatene til tyngdepunktet til hver figur.

   Regn ut koordinatene til tyngdepunktet til hver figur.

   Beregn arealet til hver figur.

   Beregn koordinatene til tyngdepunktet til hele figuren ved å bruke formlene (posisjonen til tyngdepunktet er plottet på tegningen av figuren):

Installasjonen for eksperimentelt å bestemme koordinatene til tyngdepunktet ved hjelp av hengemetoden består av vertikalt stativ 1 (se figur) som nålen er festet til 2 . Flat figur 3 Laget av papp, som er lett å slå hull i. Hull EN Og I gjennomboret på tilfeldig plasserte punkter (fortrinnsvis i lengst avstand fra hverandre). En flat figur er hengt opp på en nål, først ved et punkt EN , og så på punktet I . Ved hjelp av lodd 4 , festet til samme nål, tegn en vertikal linje på figuren med en blyant som tilsvarer tråden til loddet. Tyngdepunkt MED figuren vil være plassert i skjæringspunktet for de vertikale linjene som er tegnet når figuren henges i punktene EN Og I .

Merk. Tyngdepunktet til en symmetrisk figur er på symmetriaksen.

Tyngdepunktet til stangen er midt i høyden. Følgende metoder brukes for å løse problemer:

1. symmetrimetode: tyngdepunktet til symmetriske figurer er på symmetriaksen;

2. separasjonsmetode: komplekse seksjoner er delt inn i flere enkle deler, hvor posisjonen til tyngdepunktene er lett å bestemme;

3. negativ arealmetode: hulrom (hull) betraktes som en del av en seksjon med negativ areal.

Eksempler på problemløsning

Eksempel 1. Bestem posisjonen til tyngdepunktet til figuren vist i fig. 8.4.

Løsning

Vi deler figuren inn i tre deler:

Definert tilsvarende på C = 4,5 cm.

Eksempel 2. Finn posisjonen til tyngdepunktet til en symmetrisk stangstol ADBE(Fig. 116), hvis dimensjoner er som følger: AB = 6m, DE = 3 m og EF = 1m.

Løsning

Siden fagverket er symmetrisk, ligger tyngdepunktet på symmetriaksen D.F. Med det valgte (fig. 116) koordinataksesystemet, abscissen til fagverkets tyngdepunkt

Følgelig er bare ordinaten ukjent på C gårdens tyngdepunkt. For å bestemme det deler vi fagverket i separate deler (stenger). Lengdene deres bestemmes fra de tilsvarende trekantene.

Fra ΔAEF vi har

Fra ΔADF vi har

Tyngdepunktet til hver stang ligger i midten av koordinatene til disse sentrene er lett å bestemme ut fra tegningen (fig. 116).

De funnet lengdene og ordinatene til tyngdepunktene til individuelle deler av fagverket er lagt inn i tabellen og i henhold til formelen

bestemme ordinaten y s tyngdepunktet til et gitt flatt fagverk.

Derfor tyngdepunktet MED hele fagverket ligger på aksen DF symmetri av fagverket i en avstand på 1,59 m fra punktet F.

Eksempel 3. Bestem koordinatene til tyngdepunktet til den sammensatte seksjonen. Seksjonen består av en plate og rullede profiler (fig. 8.5).

Merk. Ofte er rammer sveiset fra forskjellige profiler, og skaper nødvendig design. Dermed reduseres metallforbruket og det dannes en struktur med høy styrke.

For standard valsede profiler er deres egne geometriske egenskaper kjent. De er gitt i de relevante standardene.

Løsning

1. La oss angi tallene med tall og skrive ut de nødvendige dataene fra tabellene:

1 - kanal nr. 10 (GOST 8240-89); høyde h = 100 mm; hyllebredde b= 46 mm; tverrsnittsareal A 1= 10,9 cm2;

2 - I-bjelke nr. 16 (GOST 8239-89); høyde 160 mm; hyllebredde 81 mm; tverrsnittsareal A 2 - 20,2 cm 2;

3 - ark 5x100; tykkelse 5 mm; bredde 100 mm; tverrsnittsareal A 3 = 0,5 10 = 5 cm 2.

2. Koordinatene til tyngdepunktene til hver figur kan bestemmes fra tegningen.

Den sammensatte seksjonen er symmetrisk, så tyngdepunktet er på symmetriaksen og koordinaten X C = 0.

3. Bestemmelse av tyngdepunktet til en sammensatt seksjon:

Eksempel 4. Bestem koordinatene til tyngdepunktet til seksjonen vist i fig. 8, EN. Seksjonen består av to vinkler 56x4 og kanal nr. 18. Kontroller riktigheten av å bestemme posisjonen til tyngdepunktet. Angi dens posisjon på seksjonen.

Løsning

1. : to hjørner 56 x 4 og kanal nr. 18. La oss betegne dem 1, 2, 3 (se fig. 8, EN).

2. Vi angir tyngdepunktene hver profil, ved hjelp av tabell 1 og 4 adj. jeg, og betegne dem C 1, C 2, Fra 3.

3. Velg et system med koordinatakser. Akser på kompatibel med symmetriaksen og aksen X tegne gjennom tyngdepunktene til hjørnene.

4. Bestem koordinatene til tyngdepunktet til hele seksjonen. Siden aksen på faller sammen med symmetriaksen, så passerer den gjennom tyngdepunktet til seksjonen, derfor x s= 0. Koordinat y s vi bestemmer med formelen

Ved å bruke tabellene i vedlegget bestemmer vi arealene til hver profil og koordinatene til tyngdepunktene:

Koordinater kl 1 Og kl 2 er lik null, siden aksen X passerer gjennom tyngdepunktene til hjørnene. La oss erstatte de oppnådde verdiene i formelen for å bestemme y s:

5. La oss indikere tyngdepunktet til seksjonen i fig. 8, a og angi det med bokstaven C. La oss vise avstanden y C = 2,43 cm fra aksen X til punkt C.

Siden hjørnene er symmetrisk plassert og har samme areal og koordinater, da A 1 = A 2, y 1 = y 2. Derfor formelen for å bestemme på C kan forenkles:

6. La oss sjekke. For dette formålet aksen X La oss tegne langs den nedre kanten av hjørnehyllen (fig. 8, b). Akser på La oss la det være som i den første løsningen. Formler for å bestemme x C Og på C ikke forandre:

Arealene til profilene vil forbli de samme, men koordinatene til tyngdepunktene til vinklene og kanalene vil endres. La oss skrive dem ned:

Finn koordinaten til tyngdepunktet:

I følge de funnet koordinatene x s Og y s tegne punkt C på tegningen Posisjonen til tyngdepunktet funnet på to måter er på samme punkt. La oss sjekke det ut. Forskjell mellom koordinater y s, funnet i den første og andre løsningen er: 6,51 - 2,43 = 4,08 cm.

Dette er lik avstanden mellom x-aksen i den første og andre løsningen: 5,6 - 1,52 = 4,08 cm.

Svar: s= 2,43 cm hvis x-aksen går gjennom tyngdepunktene til hjørnene, eller y c = 6,51 cm dersom x-aksen går langs underkanten av hjørneflensen.

Eksempel 5. Bestem koordinatene til tyngdepunktet til seksjonen vist i fig. 9, EN. Seksjonen består av I-bjelke nr. 24 og kanal nr. 24a. Vis posisjonen til tyngdepunktet på seksjonen.

Løsning

1.La oss dele seksjonen inn i rullede profiler: I-bjelke og kanal. La oss betegne dem med tallene 1 og 2.

3. Vi angir tyngdepunktene til hver profil C 1 og C 2 ved bruk av applikasjonstabeller.

4. Velg et system med koordinatakser. X-aksen er kompatibel med symmetriaksen, og y-aksen er trukket gjennom tyngdepunktet til I-bjelken.

5. Bestem koordinatene til tyngdepunktet til strekningen. Koordinat y c = 0, siden aksen X faller sammen med symmetriaksen. Vi bestemmer x-koordinaten med formelen

I følge tabellen 3 og 4 adj. I og tverrsnittsdiagrammet bestemmer vi

La oss erstatte de numeriske verdiene i formelen og få

5. La oss plotte punkt C (tyngdepunktet til seksjonen) ved å bruke de funnet verdiene av x c og y c (se fig. 9, a).

Løsningen må kontrolleres uavhengig med aksene plassert som vist i fig. 9, b. Som et resultat av løsningen får vi x c = 11,86 cm Forskjellen mellom verdiene til x c for den første og andre løsningen er 11,86 - 6,11 = 5,75 cm, som er lik avstanden mellom y-aksene for den samme. løsninger b dv /2 = 5,75 cm.

Svar: x c = 6,11 cm, hvis y-aksen går gjennom tyngdepunktet til I-bjelken; x c = 11,86 cm hvis y-aksen går gjennom de venstre ytterpunktene til I-bjelken.

Eksempel 6. Jernbanekranen hviler på skinner, avstanden mellom disse er AB = 1,5 m (Fig. 1.102). Tyngdekraften til kranvognen er G r = 30 kN, tyngdepunktet til vognen er i punktet C, liggende på linjen KL for skjæringspunktet mellom vognens symmetriplan og tegningsplanet. Tyngdekraften til kranvinsjen Q l = 10 kN påføres på punktet D. Tyngdekraften til motvekten G„=20 kN påføres ved punkt E. Tyngdekraften til bommen G c = 5 kN påføres i punkt H. Kranens utstrekning i forhold til linjen KL er 2 m stabilitetskoeffisient for kranen i ubelastet tilstand og hvilken belastning F kan løftes med denne kranen, forutsatt at stabilitetskoeffisienten må være minst to.

Løsning

1. Ved avlastning står kranen i fare for å velte ved svinging rundt skinnen EN. Derfor i forhold til poenget EN stabilitetsmoment

2. Veltende moment i forhold til et punkt EN skapes av tyngdekraften til motvekten, dvs.

3. Derav stabilitetskoeffisienten til kranen i ubelastet tilstand

4. Ved lasting av kranbommen med last F det er fare for at kranen velter ved svinging nær skinne B. Derfor i forhold til punktet I stabilitetsmoment

5. Veltemoment i forhold til skinnen I

6. I henhold til forholdene for problemet er drift av kranen tillatt med en stabilitetskoeffisient k B ≥ 2, dvs.

Kontrollspørsmål og oppgaver

1. Hvorfor kan tiltrekningskreftene til jorden som virker på punkter på kroppen tas som et system av parallelle krefter?

2. Skriv ned formler for å bestemme posisjonen til tyngdepunktet til inhomogene og homogene legemer, formler for å bestemme posisjonen til tyngdepunktet til flate seksjoner.

3. Gjenta formlene for å bestemme posisjonen til tyngdepunktet til enkle geometriske former: rektangel, trekant, trapes og halvsirkel.

4.
Hva er det statiske momentet av arealet?

5. Regn ut det statiske momentet til denne figuren rundt aksen Okse. h= 30 cm; b= 120 cm; Med= 10 cm (fig. 8.6).

6. Bestem koordinatene til tyngdepunktet til den skraverte figuren (fig. 8.7). Mål er oppgitt i mm.

7. Bestem koordinaten på figur 1 av komposittsnittet (fig. 8.8).

Når du bestemmer deg, bruk referansedataene fra GOST-tabellene "Varmvalset stål" (se vedlegg 1).

For å lage håndverk, gåter, og bare for husarbeid, oppstår noen ganger en situasjon når det er nødvendig å beregne tyngdepunktet til en figur. Og hvis for de enkleste figurene, formlene for å beregne tyngdepunktet er kjent, for eksempel for en sirkel, faller tyngdepunktet sammen med sentrum av sirkelen, så mer komplekse figurer, og spesielt figurer som består av stiplede linjer, er svært vanskelig å beregne manuelt.

Hva er tyngdepunktet? Dette er et punkt på figuren som løfter den, slik at figuren forblir i samme posisjon som den lå, for eksempel på bordet. Dette er selvfølgelig en amatørmessig forklaring. Dessuten snakker vi om flate figurer. Mer riktig er dette: Tyngdepunktet til et mekanisk system er punktet i forhold til hvilket det totale momentet til gravitasjonskreftene som virker på systemet er lik null.

Kalkulatoren beregner tyngdepunktet til enhver flat figur med homogen sammensetning, bestående av stiplede linjer.

Hva trenger du som bruker å vite? Koordinatene til toppunktene til en slik polygon er påkrevd.

Hvordan bestemme tyngdepunktet?

Hvis på punktene М1(x1,y1,z1) Og М2(x2,y2,z2) parallelle krefter virker, så deler punktet M for påføring av resultanten av disse kreftene segmentet M1M2 i omvendt proporsjon med disse kreftene

Derfor vil koordinatene til punkt M være

hvis vi snakker om påvirkning av tre virkende krefter, så er formlene like og beregnes som et aritmetisk vektet gjennomsnitt

de beregnes på samme måte hvis det ved påføringspunktene for krefter ikke er tre, men for eksempel fire eller fem eller ti.

Hvis vi antar at kraften som virker på punktene vil være gravitasjon, og massen til punktene vil være den samme, så etter sammentrekninger identiske verdier, vil formelen vår for tre poeng være som følger

Her avhenger plasseringen av tyngdepunktet kun av posisjonen til punktene. Punkt () kalles det geometriske tyngdepunktet til disse punktene

Hvis figuren er symmetrisk, faller tyngdepunktet sammen med figurens geometriske sentrum. Dette gjelder for slike figurer som en firkant, sirkel, vanlig polygon, likesidet trekant og andre lignende objekter.

Og også en liten teori som vil hjelpe med å beregne tyngdepunktet til komplekse figurer.

Plasseringen av tyngdepunktet til en ren punktmasse vil ikke endres hvis en delgruppe av punktmasser i systemet erstattes med én punktmasse som er plassert ved tyngdepunktet til denne gruppen og har summen av massene som masse. av poengene til denne gruppen.

BEREGNING AV TYNGDESENTRUM I EN TREKANT VED KOORDINATER

La oss beregne tyngdepunktet til en trekantet plate med vilkårlig form og samme tykkelse.

Hvilket materiale vi skal lage den av, stål, papir eller plast, er ikke så viktig.

Trekantens tyngdepunkt er ett av syv fantastiske poeng, og er definert som skjæringspunktet mellom medianene til sidene i denne trekanten.

Hvis vi bare kjenner koordinatene til trekanten, for eksempel, kutter vi den ut av en notatbok til en firkant, så vil koordinatene til tyngdepunktet bli bestemt som følger

Ikke prøv å tilnærme denne formelen og tenk at midten av trapesen vil bli beregnet på samme måte, for eksempel ved å bruke følgende formler

Dette er usant, eller snarere usant i tilfellet når massen er fordelt i et plan mellom disse punktene (for eksempel en plate).

Hvis vi snakker om punktmasser som ligger i disse koordinatene, vil formelen for massesenteret være riktig.

BEREGNING AV TYNGDESENTRUM TIL EN trapes VED KOORDINATER

Hvordan beregner man tyngdepunktet til en trapes?

Smarte mennesker har funnet en formel for å beregne et punkt, men i den presenteres de første dataene i form av lengdene på sidene til en trapes.

Dette er formelen.

Det er ikke praktisk når vi bare kjenner koordinatene til trapesen. Men vi vil bruke metoden for å dele en trapes i to trekanter, hvor vi for hver av dem finner tyngdepunktet, og deretter, ved å beregne for to punkter (sentre), finner vi den endelige løsningen.

For hver trekant vil senteret bli beregnet ved hjelp av den velkjente formelen

Men når vi beregner det endelige punktet, må vi ta i betraktning at ved å "trekke" hver trekant til tyngdepunktet, trekker vi også sammen hele massen av overflaten som ligger mellom disse koordinatene.

Siden forholdet mellom arealet av en figur (med samme tykkelse) og masse er lineært, er det lett å anta at den endelige beregningen ikke vil være den samme