Equation of a plane. How to write an equation of a plane?
Mutual arrangement planes. Tasks

Spatial geometry is not much more complicated than “flat” geometry, and our flights in space begin with this article. To master the topic, you need to have a good understanding of vectors, in addition, it is advisable to be familiar with the geometry of the plane - there will be many similarities, many analogies, so the information will be digested much better. In a series of my lessons, the 2D world opens with an article Equation of a straight line on a plane. But now Batman has left the flat TV screen and is launching from the Baikonur Cosmodrome.

Let's start with drawings and symbols. Schematically, the plane can be drawn in the form of a parallelogram, which creates the impression of space:

The plane is infinite, but we have the opportunity to depict only a piece of it. In practice, in addition to the parallelogram, an oval or even a cloud is also drawn. For technical reasons, it is more convenient for me to depict the plane in exactly this way and in exactly this position. Real planes that we will consider in practical examples, can be positioned in any way - mentally take the drawing in your hands and rotate it in space, giving the plane any inclination, any angle.

Designations: planes are usually denoted in small Greek letters, apparently so as not to confuse them with straight line on a plane or with straight line in space. I'm used to using the letter . In the drawing it is the letter “sigma”, and not a hole at all. Although, the holey plane is certainly quite funny.

In some cases, it is convenient to use the same Greek letters with lower subscripts to designate planes, for example, .

It is obvious that the plane is uniquely defined by three different points that do not lie on the same line. Therefore, three-letter designations of planes are quite popular - by the points belonging to them, for example, etc. Often letters are enclosed in parentheses: , so as not to confuse the plane with another geometric figure.

For experienced readers I will give quick access menu:

• How to create an equation of a plane using a point and two vectors?
• How to create an equation of a plane using a point and a normal vector?

and we will not languish in long waits:

General plane equation

The general equation of the plane has the form , where the coefficients are not equal to zero at the same time.

A number of theoretical calculations and practical problems valid both for the usual orthonormal basis and for the affine basis of space (if the oil is oil, return to the lesson Linear (non) dependence of vectors. Basis of vectors). For simplicity, we will assume that all events occur in an orthonormal basis and a Cartesian rectangular coordinate system.

Now let’s practice our spatial imagination a little. It’s okay if yours is bad, now we’ll develop it a little. Even playing on nerves requires training.

In the very general case, when the numbers are not zero, the plane intersects all three coordinate axes. For example, like this:

I repeat once again that the plane continues indefinitely in all directions, and we have the opportunity to depict only part of it.

Let's consider the simplest equations of planes:

How to understand this equation? Think about it: “Z” is ALWAYS equal to zero, for any values ​​of “X” and “Y”. This is the equation of the "native" coordinate plane. Indeed, formally the equation can be rewritten as follows: , from where you can clearly see that we don’t care what values ​​“x” and “y” take, it is important that “z” is equal to zero.

Likewise:
– equation of the coordinate plane;
– equation of the coordinate plane.

Let's complicate the problem a little, consider a plane (here and further in the paragraph we assume that the numerical coefficients are not equal to zero). Let's rewrite the equation in the form: . How to understand it? “X” is ALWAYS, for any values ​​of “Y” and “Z”, equal to a certain number. This plane is parallel to the coordinate plane. For example, a plane is parallel to a plane and passes through a point.

Likewise:
– equation of a plane that is parallel to the coordinate plane;
– equation of a plane that is parallel to the coordinate plane.

Let's add members: . The equation can be rewritten as follows: , that is, “zet” can be anything. What does it mean? “X” and “Y” are connected by the relation, which draws a certain straight line in the plane (you will find out equation of a line in a plane?). Since “z” can be anything, this straight line is “replicated” at any height. Thus, the equation defines a plane parallel to the coordinate axis

Likewise:
– equation of a plane that is parallel to the coordinate axis;
– equation of a plane that is parallel to the coordinate axis.

If the free terms are zero, then the planes will directly pass through the corresponding axes. For example, the classic “direct proportionality”: . Draw a straight line in the plane and mentally multiply it up and down (since “Z” is any). Conclusion: the plane defined by the equation passes through the coordinate axis.

We complete the review: the equation of the plane passes through the origin. Well, here it is quite obvious that the point satisfies this equation.

And finally, the case shown in the drawing: – the plane is friendly with all coordinate axes, while it always “cuts off” a triangle, which can be located in any of the eight octants.

Linear inequalities in space

To understand the information you need to study well linear inequalities in the plane, because many things will be similar. The paragraph will be of a brief overview nature with several examples, since the material is quite rare in practice.

If the equation defines a plane, then the inequalities
ask half-spaces. If the inequality is not strict (the last two in the list), then the solution of the inequality, in addition to the half-space, also includes the plane itself.

Example 5

Find the unit normal vector of the plane .

Solution: A unit vector is a vector whose length is one. Let us denote this vector by . It is absolutely clear that the vectors are collinear:

First, we remove the normal vector from the equation of the plane: .

How to find a unit vector? In order to find the unit vector, you need every divide the vector coordinate by the vector length.

Let's rewrite the normal vector in the form and find its length:

According to the above:

Answer:

Verification: what was required to be verified.

Readers who carefully studied the last paragraph of the lesson probably noticed that the coordinates of the unit vector are exactly the direction cosines of the vector:

Let's take a break from the problem at hand: when you are given an arbitrary non-zero vector, and according to the condition it is required to find its direction cosines (see the last problems of the lesson Dot product of vectors), then you, in fact, find a unit vector collinear to this one. Actually two tasks in one bottle.

The need to find the unit normal vector arises in some problems of mathematical analysis.

We’ve figured out how to fish out a normal vector, now let’s answer the opposite question:

How to create an equation of a plane using a point and a normal vector?

This rigid construction of a normal vector and a point is well known to the dartboard. Please stretch your hand forward and mentally select an arbitrary point in space, for example, a small cat in the sideboard. Obviously, through this point you can draw a single plane perpendicular to your hand.

The equation of a plane passing through a point perpendicular to the vector is expressed by the formula:

In order for a single plane to be drawn through any three points in space, it is necessary that these points do not lie on the same straight line.

Consider the points M 1 (x 1, y 1, z 1), M 2 (x 2, y 2, z 2), M 3 (x 3, y 3, z 3) in the general Cartesian coordinate system.

In order for an arbitrary point M(x, y, z) to lie in the same plane with points M 1, M 2, M 3, it is necessary that the vectors be coplanar.

(
) = 0

Thus,

Equation of a plane passing through three points:

Equation of a plane given two points and a vector collinear to the plane.

Let the points M 1 (x 1,y 1,z 1),M 2 (x 2,y 2,z 2) and the vector be given
.

Let's create an equation for a plane passing through the given points M 1 and M 2 and an arbitrary point M (x, y, z) parallel to the vector .

Vectors
and vector
must be coplanar, i.e.

(
) = 0

Plane equation:

Equation of a plane using one point and two vectors,

collinear to the plane.

Let two vectors be given
And
, collinear planes. Then for an arbitrary point M(x, y, z) belonging to the plane, the vectors
must be coplanar.

Plane equation:

Equation of a plane by point and normal vector .

Theorem. If a point M is given in space 0 (X 0 , y 0 , z 0 ), then the equation of the plane passing through the point M 0 perpendicular to the normal vector (A, B, C) has the form:

A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Proof. For an arbitrary point M(x, y, z) belonging to the plane, we compose a vector. Because vector is the normal vector, then it is perpendicular to the plane, and, therefore, perpendicular to the vector
. Then the scalar product

= 0

Thus, we obtain the equation of the plane

The theorem has been proven.

Equation of a plane in segments.

If in the general equation Ax + Bi + Cz + D = 0 we divide both sides by (-D)

,

replacing
, we obtain the equation of the plane in segments:

The numbers a, b, c are the intersection points of the plane with the x, y, z axes, respectively.

Equation of a plane in vector form.

Where

- radius vector of the current point M(x, y, z),

A unit vector having the direction of a perpendicular dropped onto a plane from the origin.

,  and  are the angles formed by this vector with the x, y, z axes.

p is the length of this perpendicular.

In coordinates, this equation looks like:

xcos + ycos + zcos - p = 0.

Distance from a point to a plane.

The distance from an arbitrary point M 0 (x 0, y 0, z 0) to the plane Ax+By+Cz+D=0 is:

Example. Find the equation of the plane, knowing that point P(4; -3; 12) is the base of the perpendicular dropped from the origin to this plane.

So A = 4/13; B = -3/13; C = 12/13, we use the formula:

A(x – x 0 ) + B(y – y 0 ) + C(z – z 0 ) = 0.

Example. Find the equation of a plane passing through two points P(2; 0; -1) and

Q(1; -1; 3) perpendicular to the plane 3x + 2y – z + 5 = 0.

Normal vector to the plane 3x + 2y – z + 5 = 0
parallel to the desired plane.

We get:

Example. Find the equation of the plane passing through points A(2, -1, 4) and

B(3, 2, -1) perpendicular to the plane X + at + 2z – 3 = 0.

The required equation of the plane has the form: A x+B y+C z+ D = 0, normal vector to this plane (A, B, C). Vector
(1, 3, -5) belongs to the plane. The plane given to us, perpendicular to the desired one, has a normal vector (1, 1, 2). Because points A and B belong to both planes, and the planes are mutually perpendicular, then

So the normal vector (11, -7, -2). Because point A belongs to the desired plane, then its coordinates must satisfy the equation of this plane, i.e. 112 + 71 - 24 +D= 0;D= -21.

In total, we get the equation of the plane: 11 x - 7y – 2z – 21 = 0.

Example. Find the equation of the plane, knowing that point P(4, -3, 12) is the base of the perpendicular dropped from the origin to this plane.

Finding the coordinates of the normal vector
= (4, -3, 12). The required equation of the plane has the form: 4 x – 3y + 12z+ D = 0. To find the coefficient D, we substitute the coordinates of point P into the equation:

16 + 9 + 144 + D = 0

In total, we get the required equation: 4 x – 3y + 12z – 169 = 0

Example. Given are the coordinates of the vertices of the pyramid A 1 (1; 0; 3), A 2 (2; -1; 3), A 3 (2; 1; 1),

Find the length of edge A 1 A 2.

Find the angle between edges A 1 A 2 and A 1 A 4.

Find the angle between edge A 1 A 4 and face A 1 A 2 A 3.

First we find the normal vector to the face A 1 A 2 A 3 How vector product vectors
And
.

= (2-1; 1-0; 1-3) = (1; 1; -2);

Let's find the angle between the normal vector and the vector
.

-4 – 4 = -8.

The desired angle  between the vector and the plane will be equal to  = 90 0 - .

Find the area of ​​face A 1 A 2 A 3.

Find the volume of the pyramid.

Find the equation of the plane A 1 A 2 A 3.

Let's use the formula for the equation of a plane passing through three points.

2x + 2y + 2z – 8 = 0

x + y + z – 4 = 0;

When using the computer version “ Higher mathematics course” you can run a program that will solve the above example for any coordinates of the vertices of the pyramid.

To start the program, double-click on the icon:

In the program window that opens, enter the coordinates of the vertices of the pyramid and press Enter. In this way, all decision points can be obtained one by one.

Note: To run the program, the Maple program ( Waterloo Maple Inc.) of any version, starting with MapleV Release 4, must be installed on your computer.

Let us consider the plane Q in space. Its position is completely determined by specifying the vector N perpendicular to this plane and some fixed point lying in the Q plane. The vector N perpendicular to the Q plane is called the normal vector of this plane. If we denote by A, B and C the projections of the normal vector N, then

Let us derive the equation of the plane Q passing through a given point and having a given normal vector . To do this, consider a vector connecting a point with an arbitrary point on the Q plane (Fig. 81).

For any position of point M on the plane Q, the vector MHM is perpendicular to the normal vector N of the plane Q. Therefore, the scalar product Let us write the scalar product in terms of projections. Since , and is a vector, then

and therefore

We have shown that the coordinates of any point in the Q plane satisfy equation (4). It is easy to see that the coordinates of points not lying on the Q plane do not satisfy this equation (in the latter case). Consequently, we have obtained the required equation for the plane Q. Equation (4) is called the equation of the plane passing through a given point. It is of the first degree relative to the current coordinates

So, we have shown that every plane corresponds to an equation of the first degree with respect to the current coordinates.

Example 1. Write the equation of a plane passing through a point perpendicular to the vector.

Solution. Here . Based on formula (4) we obtain

or, after simplification,

Giving coefficients A, B and C to equation (4) different meanings, we can obtain the equation of any plane passing through the point . The set of planes passing through a given point is called a bundle of planes. Equation (4), in which the coefficients A, B and C can take any values, is called the equation of a bunch of planes.

Example 2. Create an equation for a plane passing through three points (Fig. 82).

Solution. Let's write the equation for a bunch of planes passing through the point

ANGLE BETWEEN PLANES

Consider two planes α 1 and α 2, defined respectively by the equations:

Under angle between two planes we will understand one of the dihedral angles formed by these planes. It is obvious that the angle between the normal vectors and planes α 1 and α 2 is equal to one of the indicated adjacent dihedral angles or . That's why . Because And , That

.

Example. Determine the angle between planes x+2y-3z+4=0 and 2 x+3y+z+8=0.

Condition for parallelism of two planes.

Two planes α 1 and α 2 are parallel if and only if their normal vectors are parallel, and therefore .

So, two planes are parallel to each other if and only if the coefficients of the corresponding coordinates are proportional:

or

Condition of perpendicularity of planes.

It is clear that two planes are perpendicular if and only if their normal vectors are perpendicular, and therefore, or .

Thus, .

Examples.

STRAIGHT IN SPACE.

VECTOR EQUATION FOR A LINE.

PARAMETRIC DIRECT EQUATIONS

The position of a line in space is completely determined by specifying any of its fixed points M 1 and a vector parallel to this line.

A vector parallel to a line is called guides vector of this line.

So let the straight line l passes through a point M 1 (x 1 , y 1 , z 1), lying on a line parallel to the vector .

Consider an arbitrary point M(x,y,z) on a straight line. From the figure it is clear that .

Vectors and are collinear, so there is such a number t, what , where is the multiplier t can take any numeric value depending on the position of the point M on a straight line. Factor t called a parameter. Having designated the radius vectors of points M 1 and M respectively, through and , we obtain . This equation is called vector equation of a straight line. It shows that for each parameter value t corresponds to the radius vector of some point M, lying on a straight line.

Let's write this equation in coordinate form. Notice, that , and from here

The resulting equations are called parametric equations of a straight line.

When changing a parameter t coordinates change x, y And z and period M moves in a straight line.

CANONICAL EQUATIONS OF THE DIRECT

Let M 1 (x 1 , y 1 , z 1) – a point lying on a straight line l, And is its direction vector. Let us again take an arbitrary point on the line M(x,y,z) and consider the vector .

It is clear that the vectors are also collinear, so their corresponding coordinates must be proportional, therefore,

– canonical equations of a straight line.

Note 1. Note that the canonical equations of the line could be obtained from the parametric ones by eliminating the parameter t. Indeed, from the parametric equations we obtain or .

Example. Write down the equation of the line in parametric form.

Let's denote , from here x = 2 + 3t, y = –1 + 2t, z = 1 –t.

Note 2. Let the straight line be perpendicular to one of the coordinate axes, for example the axis Ox. Then the direction vector of the line is perpendicular Ox, hence, m=0. Consequently, the parametric equations of the line will take the form

Excluding the parameter from the equations t, we obtain the equations of the line in the form

However, in this case too, we agree to formally write the canonical equations of the line in the form . Thus, if the denominator of one of the fractions is zero, this means that the straight line is perpendicular to the corresponding coordinate axis.

Likewise, canonical equations corresponds to a straight line perpendicular to the axes Ox And Oy or parallel to the axis Oz.

Examples.

GENERAL EQUATIONS OF A STRAIGHT LINE AS LINES OF INTERSECTION OF TWO PLANES

Through every straight line in space there are countless planes. Any two of them, intersecting, define it in space. Consequently, the equations of any two such planes, considered together, represent the equations of this line.

In general, any two non-parallel planes given by the general equations

determine the straight line of their intersection. These equations are called general equations straight.

Examples.

Construct a line given by the equations

To construct a straight line, it is enough to find any two of its points. The easiest way is to select the points of intersection of a straight line with coordinate planes. For example, the point of intersection with the plane xOy we obtain from the equations of the straight line, assuming z= 0:

Having solved this system, we find the point M 1 (1;2;0).

Similarly, assuming y= 0, we get the point of intersection of the line with the plane xOz:

From the general equations of a straight line one can move on to its canonical or parametric equations. To do this you need to find some point M 1 on a straight line and the direction vector of a straight line.

Point coordinates M 1 we obtain from this system of equations, giving one of the coordinates an arbitrary value. To find the direction vector, note that this vector must be perpendicular to both normal vectors And . Therefore, beyond the direction vector of the straight line l you can take the vector product of normal vectors:

.

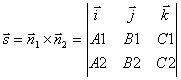Example. Give general equations of the line to the canonical form.

Let's find a point lying on a line. To do this, we choose arbitrarily one of the coordinates, for example, y= 0 and solve the system of equations:

The normal vectors of the planes defining the line have coordinates Therefore, the direction vector will be straight

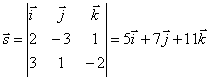. Hence, l: .

ANGLE BETWEEN STRAIGHTS

Angle between straight lines in space we will call any of the adjacent angles formed by two straight lines drawn through an arbitrary point parallel to the data.

Let two lines be given in space:

Obviously, the angle φ between straight lines can be taken as the angle between their direction vectors and . Since , then using the formula for the cosine of the angle between vectors we get

You can set different ways(one point and a vector, two points and a vector, three points, etc.). It is with this in mind that the equation of the plane can have different kinds. Also, subject to certain conditions, planes can be parallel, perpendicular, intersecting, etc. We'll talk about this in this article. We will learn how to create a general equation of a plane and more.

Normal form of equation

Let's say there is a space R 3 that has a rectangular XYZ coordinate system. Let us define the vector α, which will be released from the initial point O. Through the end of the vector α we draw a plane P, which will be perpendicular to it.

Let us denote an arbitrary point on P as Q = (x, y, z). Let's sign the radius vector of point Q with the letter p. In this case, the length of the vector α is equal to р=IαI and Ʋ=(cosα,cosβ,cosγ).

This is a unit vector that is directed to the side, like the vector α. α, β and γ are the angles that are formed between the vector Ʋ and the positive directions of the space axes x, y, z, respectively. The projection of any point QϵП onto the vector Ʋ is constant value, which is equal to p: (p,Ʋ) = p(p≥0).

The above equation makes sense when p=0. The only thing is that the plane P in this case will intersect the point O (α=0), which is the origin of coordinates, and the unit vector Ʋ released from the point O will be perpendicular to P, despite its direction, which means that the vector Ʋ is determined with accurate to the sign. The previous equation is the equation of our plane P, expressed in vector form. But in coordinates it will look like this:

P here is greater than or equal to 0. We have found the equation of the plane in space in normal form.

General equation

If we multiply the equation in coordinates by any number that is not equal to zero, we obtain an equation equivalent to this one, defining that very plane. It will look like this:

Here A, B, C are numbers that are simultaneously different from zero. This equation is called the general plane equation.

Equations of planes. Special cases

Equation in general view may be modified subject to additional conditions. Let's look at some of them.

Let's assume that the coefficient A is 0. This means that this plane is parallel to the given Ox axis. In this case, the form of the equation will change: Ву+Cz+D=0.

Similarly, the form of the equation will change under the following conditions:

• Firstly, if B = 0, then the equation will change to Ax + Cz + D = 0, which will indicate parallelism to the Oy axis.
• Secondly, if C=0, then the equation will be transformed into Ax+By+D=0, which will indicate parallelism to the given Oz axis.
• Thirdly, if D=0, the equation will look like Ax+By+Cz=0, which will mean that the plane intersects O (the origin).
• Fourth, if A=B=0, then the equation will change to Cz+D=0, which will prove parallel to Oxy.
• Fifthly, if B=C=0, then the equation becomes Ax+D=0, which means that the plane to Oyz is parallel.
• Sixth, if A=C=0, then the equation will take the form Ву+D=0, that is, it will report parallelism to Oxz.

Type of equation in segments

In the case when the numbers A, B, C, D are different from zero, the form of equation (0) can be as follows:

x/a + y/b + z/c = 1,

in which a = -D/A, b = -D/B, c = -D/C.

We get as a result. It is worth noting that this plane will intersect the Ox axis at a point with coordinates (a,0,0), Oy - (0,b,0), and Oz - (0,0,c).

Taking into account the equation x/a + y/b + z/c = 1, it is not difficult to visually imagine the placement of the plane relative to a given coordinate system.

Normal vector coordinates

The normal vector n to the plane P has coordinates that are coefficients of the general equation of this plane, that is, n (A, B, C).

In order to determine the coordinates of the normal n, it is enough to know the general equation of a given plane.

When using an equation in segments, which has the form x/a + y/b + z/c = 1, as when using a general equation, you can write the coordinates of any normal vector of a given plane: (1/a + 1/b + 1/ With).

It is worth noting that the normal vector helps solve a variety of problems. The most common ones include problems that involve proving the perpendicularity or parallelism of planes, problems of finding angles between planes or angles between planes and straight lines.

Type of plane equation according to the coordinates of the point and normal vector

A nonzero vector n perpendicular to a given plane is called normal for a given plane.

Let us assume that in the coordinate space (rectangular coordinate system) Oxyz are given:

• point Mₒ with coordinates (xₒ,yₒ,zₒ);
• zero vector n=A*i+B*j+C*k.

It is necessary to create an equation for a plane that will pass through the point Mₒ perpendicular to the normal n.

We choose any arbitrary point in space and denote it M (x y, z). Let the radius vector of any point M (x,y,z) be r=x*i+y*j+z*k, and the radius vector of the point Mₒ (xₒ,yₒ,zₒ) - rₒ=xₒ*i+yₒ *j+zₒ*k. Point M will belong to a given plane if the vector MₒM is perpendicular to vector n. Let us write the orthogonality condition using the scalar product:

[MₒM, n] = 0.

Since MₒM = r-rₒ, the vector equation of the plane will look like this:

This equation can have another form. To do this, the properties of the scalar product are used, and the transformation is left-hand side equations = - . If we denote it as c, we get the following equation: - c = 0 or = c, which expresses the constancy of the projections onto the normal vector of the radius vectors of given points that belong to the plane.

Now we can get the coordinate form of writing the vector equation of our plane = 0. Since r-rₒ = (x-xₒ)*i + (y-yₒ)*j + (z-zₒ)*k, and n = A*i+B *j+С*k, we have:

It turns out that we have an equation for a plane passing through a point perpendicular to the normal n:

A*(x- xₒ)+B*(y- yₒ)C*(z-zₒ)=0.

Type of plane equation according to the coordinates of two points and a vector collinear to the plane

Let us define two arbitrary points M′ (x′,y′,z′) and M″ (x″,y″,z″), as well as a vector a (a′,a″,a‴).

Now we can create an equation for a given plane that will pass through the existing points M′ and M″, as well as any point M with coordinates (x, y, z) parallel to the given vector a.

In this case, the vectors M′M=(x-x′;y-y′;z-z′) and M″M=(x″-x′;y″-y′;z″-z′) must be coplanar with the vector a=(a′,a″,a‴), which means that (M′M, M″M, a)=0.

So, our plane equation in space will look like this:

Type of equation of a plane intersecting three points

Let's say we have three points: (x′,y′,z′), (x″,y″,z″), (x‴,y‴,z‴), which do not belong to the same line. It is necessary to write the equation of a plane passing through given three points. The theory of geometry claims that this kind of plane really exists, but it is the only one and unique. Since this plane intersects the point (x′,y′,z′), the form of its equation will be as follows:

Here A, B, C are different from zero at the same time. Also, the given plane intersects two more points: (x″,y″,z″) and (x‴,y‴,z‴). In this regard, the following conditions must be met:

Now we can create a homogeneous system with unknowns u, v, w:

In our case x,y or z acts as an arbitrary point that satisfies equation (1). Given equation (1) and the system of equations (2) and (3), the system of equations indicated in the figure above is satisfied by the vector N (A,B,C), which is non-trivial. That is why the determinant of this system is equal to zero.

Equation (1) that we have obtained is the equation of the plane. It passes through 3 points exactly, and this is easy to check. To do this, we need to expand our determinant into the elements in the first row. From the existing properties of the determinant it follows that our plane simultaneously intersects three initially given points (x′,y′,z′), (x″,y″,z″), (x‴,y‴,z‴). That is, we have solved the task assigned to us.

Dihedral angle between planes

A dihedral angle represents a spatial geometric figure, formed by two half-planes that emanate from one straight line. In other words, this is the part of space that is limited by these half-planes.

Let's say we have two planes with the following equations:

We know that the vectors N=(A,B,C) and N¹=(A¹,B¹,C¹) are perpendicular according to the given planes. In this regard, the angle φ between the vectors N and N¹ is equal to the angle (dihedral) that is located between these planes. The dot product has the form:

NN¹=|N||N¹|cos φ,

precisely because

cosφ= NN¹/|N||N¹|=(AA¹+BB¹+CC¹)/((√(A²+B²+C²))*(√(A¹)²+(B¹)²+(C¹)²)).

It is enough to take into account that 0≤φ≤π.

In fact, two planes that intersect form two angles (dihedral): φ 1 and φ 2. Their sum is equal to π (φ 1 + φ 2 = π). As for their cosines, their absolute values ​​are equal, but they differ in sign, that is, cos φ 1 = -cos φ 2. If in equation (0) we replace A, B and C with the numbers -A, -B and -C, respectively, then the equation that we get will determine the same plane, the only one, the angle φ in the equation cos φ= NN 1 /| N||N 1 | will be replaced by π-φ.

Equation of a perpendicular plane

Planes between which the angle is 90 degrees are called perpendicular. Using the material presented above, we can find the equation of a plane perpendicular to another. Let's say we have two planes: Ax+By+Cz+D=0 and A¹x+B¹y+C¹z+D=0. We can say that they will be perpendicular if cosφ=0. This means that NN¹=AA¹+BB¹+CC¹=0.

Parallel plane equation

Two planes that do not contain common points are called parallel.

The condition (their equations are the same as in the previous paragraph) is that the vectors N and N¹, which are perpendicular to them, are collinear. This means that the following proportionality conditions are met:

A/A¹=B/B¹=C/C¹.

If the proportionality conditions are extended - A/A¹=B/B¹=C/C¹=DD¹,

this indicates that these planes coincide. This means that the equations Ax+By+Cz+D=0 and A¹x+B¹y+C¹z+D¹=0 describe one plane.

Distance to plane from point

Let's say we have a plane P, which is given by equation (0). It is necessary to find the distance to it from a point with coordinates (xₒ,yₒ,zₒ)=Qₒ. To do this, you need to bring the equation of the plane P into normal form:

(ρ,v)=р (р≥0).

IN in this caseρ (x,y,z) is the radius vector of our point Q located on P, p is the length of the perpendicular P that was released from the zero point, v is the unit vector, which is located in the direction a.

The difference ρ-ρº radius vector of some point Q = (x, y, z), belonging to P, as well as the radius vector of a given point Q 0 = (xₒ, уₒ, zₒ) is such a vector, the absolute value of the projection of which onto v equals the distance d that needs to be found from Q 0 = (xₒ,уₒ,zₒ) to P:

D=|(ρ-ρ 0 ,v)|, but

(ρ-ρ 0 ,v)= (ρ,v)-(ρ 0 ,v) =р-(ρ 0 ,v).

So it turns out

d=|(ρ 0 ,v)-р|.

Thus, we will find the absolute value of the resulting expression, that is, the desired d.

Using the parameter language, we get the obvious:

d=|Ахₒ+Вуₒ+Czₒ|/√(А²+В²+С²).

If set point Q 0 is on the other side of the plane P, like the origin of coordinates, then between the vector ρ-ρ 0 and v is therefore located:

d=-(ρ-ρ 0 ,v)=(ρ 0 ,v)-р>0.

In the case when the point Q 0, together with the origin of coordinates, is located on the same side of P, then the created angle is acute, that is:

d=(ρ-ρ 0 ,v)=р - (ρ 0 , v)>0.

As a result, it turns out that in the first case (ρ 0 ,v)>р, in the second (ρ 0 ,v)<р.

Tangent plane and its equation

The tangent plane to the surface at the point of contact Mº is a plane containing all possible tangents to the curves drawn through this point on the surface.

With this type of surface equation F(x,y,z)=0, the equation of the tangent plane at the tangent point Mº(xº,yº,zº) will look like this:

F x (xº,yº,zº)(x- xº)+ F x (xº, yº, zº)(y- yº)+ F x (xº, yº,zº)(z-zº)=0.

If you specify the surface in explicit form z=f (x,y), then the tangent plane will be described by the equation:

z-zº =f(xº, yº)(x- xº)+f(xº, yº)(y- yº).

Intersection of two planes

In the coordinate system (rectangular) Oxyz is located, two planes П′ and П″ are given, which intersect and do not coincide. Since any plane located in a rectangular coordinate system is determined by a general equation, we will assume that P′ and P″ are given by the equations A′x+B′y+C′z+D′=0 and A″x+B″y+ С″z+D″=0. In this case, we have the normal n′ (A′,B′,C′) of the plane P′ and the normal n″ (A″,B″,C″) of the plane P″. Since our planes are not parallel and do not coincide, these vectors are not collinear. Using the language of mathematics, we can write this condition as follows: n′≠ n″ ↔ (A′,B′,C′) ≠ (λ*A″,λ*B″,λ*C″), λϵR. Let the straight line that lies at the intersection of P′ and P″ be denoted by the letter a, in this case a = P′ ∩ P″.

a is a straight line consisting of the set of all points of the (common) planes P′ and P″. This means that the coordinates of any point belonging to line a must simultaneously satisfy the equations A′x+B′y+C′z+D′=0 and A″x+B″y+C″z+D″=0. This means that the coordinates of the point will be a partial solution of the following system of equations:

As a result, it turns out that the (general) solution of this system of equations will determine the coordinates of each of the points of the line, which will act as the intersection point of P′ and P″, and determine the straight line a in the Oxyz (rectangular) coordinate system in space.