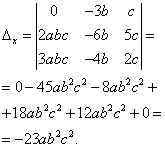Consider a system of 3 equations with three unknowns
Using 3rd order determinants, the solution to such a system can be written in the same form as for a system of two equations, i.e.
(2.4)
if 0. Here
It's there Cramer's rule solving a system of three linear equations in three unknowns.
Example 2.3. Solve a system of linear equations using Cramer's rule:
Solution . Finding the determinant of the main matrix of the system
Since 0, then to find a solution to the system we can apply Cramer’s rule, but first we calculate three more determinants:
Examination:
Therefore, the solution was found correctly.
Cramer's rules obtained for linear systems of 2nd and 3rd order suggest that the same rules can be formulated for linear systems of any order. Really happens
Cramer's theorem. Quadratic system of linear equations with a nonzero determinant of the main matrix of the system (0) has one and only one solution and this solution is calculated using the formulas
(2.5)
Where – determinant of the main matrix, i – matrix determinant, obtained from the main one, replacingith column column of free terms.
Note that if =0, then Cramer’s rule does not apply. This means that the system either has no solutions at all or has infinitely many solutions.
Having formulated Cramer's theorem, the question naturally arises of calculating determinants of higher orders.
2.4. Determinants of nth order
Additional minor M ij element a ij is a determinant obtained from a given by deleting i th line and j th column. Algebraic complement A ij element a ij the minor of this element taken with the sign (–1) is called i + j, i.e. A ij = (–1) i + j M ij .
For example, let's find the minors and algebraic complements of the elements a 23 and a 31 qualifiers
We get
Using the concept of algebraic complement we can formulate determinant expansion theoremn-th order by row or column.
Theorem 2.1. Matrix determinantAis equal to the sum of the products of all elements of a certain row (or column) by their algebraic complements:
(2.6)
This theorem underlies one of the main methods for calculating determinants, the so-called. order reduction method. As a result of the expansion of the determinant n th order over any row or column, we get n determinants ( n–1)th order. To have fewer such determinants, it is advisable to select the row or column that has the most zeros. In practice, the expansion formula for the determinant is usually written as:
those. algebraic additions are written explicitly in terms of minors.
Examples 2.4. Calculate the determinants by first sorting them into some row or column. Typically, in such cases, select the column or row that has the most zeros. The selected row or column will be indicated by an arrow.
2.5. Basic properties of determinants
Expanding the determinant over any row or column, we get n determinants ( n–1)th order. Then each of these determinants ( n–1)th order can also be decomposed into a sum of determinants ( n–2)th order. Continuing this process, one can reach the 1st order determinants, i.e. to the elements of the matrix whose determinant is calculated. So, to calculate 2nd order determinants, you will have to calculate the sum of two terms, for 3rd order determinants - the sum of 6 terms, for 4th order determinants - 24 terms. The number of terms will increase sharply as the order of the determinant increases. This means that calculating determinants of very high orders becomes a rather labor-intensive task, beyond the capabilities of even a computer. However, determinants can be calculated in another way, using the properties of determinants.
Property 1 . The determinant will not change if the rows and columns in it are swapped, i.e. when transposing a matrix:
.
This property indicates the equality of the rows and columns of the determinant. In other words, any statement about the columns of a determinant is also true for its rows and vice versa.
Property 2 . The determinant changes sign when two rows (columns) are interchanged.
Consequence . If a determinant has two identical rows (columns), then it equal to zero.
Property 3 . The common factor of all elements in any row (column) can be taken out of the determinant sign.
For example,
Consequence . If all elements of a certain row (column) of a determinant are equal to zero, then the determinant itself is equal to zero.
Property 4 . The determinant will not change if the elements of one row (column) are added to the elements of another row (column), multiplied by any number.
For example,
Property 5 . The determinant of the product of matrices is equal to the product of the determinants of matrices:
Gabriel Kramer – mathematician, creator of the method of the same name for solving systems of linear equations
Gabriel Cramer is a famous mathematician who was born on July 31, 1704. Even as a child, Gabriel amazed with his intellectual abilities, especially in the field of mathematics. When Kramer was 20 years old, he took a job as a full-time teacher at the University of Geneva.
While traveling around Europe, Gabriel met the mathematician Johann Bernoulli, who became his mentor. It was only thanks to Johann that Kramer wrote many articles on geometry, the history of mathematics and philosophy. And in my free time from work, I studied mathematics more and more.
Finally, the day came when Cramer found a way with which it would be possible to easily solve not only easy, but also complex systems of linear equations.
In 1740, Cramer published several works where the solution of square matrices was clearly presented and an algorithm was described for how to find the inverse matrix. Next, the mathematician described finding linear equations of varying complexity, where his formulas can be applied. That’s why the topic was called: “Solving systems of linear equations using Cramer’s method.”
The scientist died at the age of 48 (in 1752). He had many more plans, but, unfortunately, he never managed to implement them.
Let a system of linear equations of this form be given:
where , , are unknown variables, are numerical coefficients, and are free terms.
The solution of SLAEs (systems of linear algebraic equations) are those unknown values for which all equations of a given system are transformed into identities.
If we write the system in matrix form, then we get , where
This main matrix contains elements whose coefficients for unknown variables,
This is a column matrix of free terms, but there is also a column matrix of unknown variables:
After the unknown variables are found, the matrix will be the solution to the system of equations, and our equality will be transformed into an identity. . If you multiply, then . It turns out: .
If the matrix is non-singular, that is, its determinant is not equal to zero, then the SLAE has only one the only solution, which is found using Cramer's method.
As a rule, to solve systems of linear equations using the Cramer method, you need to pay attention to two properties on which this method is based:
1. The determinant of a square matrix is equal to the sum of the products of the elements of any of the rows (columns) and their algebraic complements:
Here – 1, 2, …, n; – 1, 2, 3, …, n.
2. The sum of the products of the elements of a given matrix of any row or any column by the algebraic complements of certain elements of the second row (column) is equal to zero:
where – 1, 2, …, n; – 1, 2, 3, …, n. .
So now we can find the first unknown. To do this, it is necessary to multiply both sides of the first equation of the system by, parts of the second equation by, both sides of the third equation by, etc. That is, each equation of one system must be multiplied by certain algebraic complements of the first column of the matrix:
Now let’s add all the left-hand sides of the equation, group the terms, taking into account the unknown variables, and equate the same sum to the sum of the right-hand sides of the equation system:
We can turn to the properties of determinants described above and then we get:
And the previous equality already looks like this:
This is where it comes from.
We find similarly. To do this, you need to multiply both sides of the equations by algebraic additions, which are in the second column of the matrix.
Now you need to add up all the equations of the system and group the terms for unknown variables. To do this, recall the properties of the determinant:
Where does it come from?
All other unknown variables are found similarly.
If we designate:
then formulas are obtained, thanks to which unknown variables are found using Cramer’s method:
Comment.
A trivial solution for can only exist if the system of equations is homogeneous. Indeed, if all free terms are zero, then the determinants are zero, since they contain a column with zero elements. Of course, then the formulas , , will give
Cramer's method - theorems
Before solving the equation, you need to know:
- cancellation theorem;
- substitution theorem.
Substitution theorem
Theorem
The sum of the products of algebraic additions of any column (row) by arbitrary numbers is equal to a new determinant, in which these numbers replace the corresponding elements of the original determinant, which correspond to these algebraic additions.
For example,
where are the algebraic complements of the elements of the first column of the original determinant:
Cancellation theorem
Theorem
The sum of the products of elements of one row (column) by the algebraic complements of the corresponding elements of another row (column) is equal to zero.
For example:
Algorithm for solving equations using Cramer's method
Cramer's method is a simple way to solve systems of linear algebraic equations. This option applies exclusively to SLAEs in which the number of equations coincides with the number of unknowns, and the determinant is nonzero.
So, when you have learned all the stages, you can move on to the algorithm for solving equations using Cramer’s method. Let's write it down sequentially:
Step 1. Calculate the main determinant of the matrix
and you need to make sure that the determinant is non-zero (not equal to zero).
Step 2. Find determinants
These are the determinants of the matrices, which were obtained from the matrix by replacing the columns with free terms.
Step 3. Calculate unknown variables
Now let’s remember Cramer’s formulas, which we use to calculate the roots (unknown variables):
Step 4. Check
We check the solution using substitution into the original SLAE. Absolutely all equations in the system must be transformed into identities. You can also calculate the product of matrices. If the resulting matrix is equal to , then the system is solved correctly. If it does not equal , most likely there is an error in one of the equations.
Let's first look at a system of two linear equations, since it is simpler and will help you understand how to correctly use Cramer's rule. If you understand simple and short equations, then you can solve more complex systems of three equations with three unknowns.
Among other things, there are systems of equations with two variables that can be solved exclusively thanks to Cramer’s rule.
So, we are given a system of two linear equations:
First, we calculate the main determinant (determinant of the system):
This means that if , then the system either has many solutions, or the system has no solutions. In this case, there is no point in using Cramer’s rule, since no solution will be obtained and you need to remember the Gauss method, with which this example solved quickly and easily.
If , then the system has only one solution, but for this it is necessary to calculate two more determinants and find the roots of the system.
Often in practice, determinants can be denoted not only by , but also by the Latin letter, which will also be correct.
It’s easy to find the roots of the equation, since the main thing is to know the formulas:
Since we were able to solve a system of two linear equations, now we can easily solve a system of three linear equations, and for this we will consider the system:
Here the algebraic complements of the elements are the first column. When deciding, do not forget about additional elements. So, in a system of linear equations you need to find three unknowns - with other elements known.
Let's create a determinant of the system from the coefficients of the unknowns:
Let us multiply each equation term by term, respectively, by , , – algebraic complements of the elements of the first column (coefficients of ) and add all three equations. We get:
According to the expansion theorem, the coefficient at is equal to . The coefficients of and will be equal to zero by the cancellation theorem. The right-hand side of the equality by the substitution theorem gives a new determinant, which is called auxiliary and denoted
After this we can write the equality:
To find and we multiply each of the equations of the original system in the first case, respectively, by , in the second - by and add. Subsequently, we obtain:
If , then as a result we obtain Cramer’s formulas:
The procedure for solving a homogeneous system of equations
A special case is homogeneous systems:
Among the solutions of a homogeneous system there can be both zero solutions and solutions different from zero.
Theorem
If the determinant of a homogeneous system (3) is nonzero, then such a system can have only one solution.
Indeed, auxiliary determinants, such as those that have a zero column and therefore, behind Cramer's formulas
Theorem
If a homogeneous system has a nonzero solution, then its determinant is zero
Indeed, let one of the unknowns, for example, be different from zero. According to homogeneity, Equality (2) will be written: . Where does it come from that
Examples of solutions using Cramer's method
Let's look at the solution using Cramer's method as an example and you will see that there is nothing complicated, but be extremely careful, because common mistakes in signs lead to an incorrect answer.
Example 1
Task
Solution
The first thing to do is calculate the determinant of the matrix:
As we see, therefore, according to Cramer’s theorem, the system has a unique solution (the system is consistent). Next, you need to calculate auxiliary determinants. To do this, replace the first column from the determinant with a column of free coefficients. It turns out:
We similarly find the remaining determinants:
And we check:
Answer
Example 2
Task
Solve the system of equations using Cramer's method:
Solution
We find the determinants:
Answer
= = = = = =
Examination
The equation has a unique solution.
Answer
Example 3
Task
Solve the system using Cramer's method
Solution
As you understand, first we find the main determinant:
As we see, the main determinant is not equal to zero and therefore the system has a unique solution. Now we can calculate the remaining determinants:
Using Cramer's formulas we find the roots of the equation:
To make sure the solution is correct, you need to check:
As we can see, having substituted the solved roots into the equation, we got the same answer as at the beginning of the problem, which indicates the right decision equations.
Answer
The system of equations has a unique solution: , , .
There are examples when the equation has no solutions. This may be the case when the determinant of the system is equal to zero, and the determinants of the unknowns are not equal to zero. In this case, they say that the system is inconsistent, that is, it has no solutions. Let's see in the following example how this can happen.
Example 4
Task
Solve a system of linear equations using the Cramer method:
Solution
As in previous examples, we find the main determinant of the system:
In this system, the determinant is equal to zero, respectively, the system is inconsistent and definite or inconsistent and has no solutions. To clarify, we need to find determinants for the unknowns as we did earlier:
We found the determinants of the unknowns and saw that all of them are not equal to zero. Therefore, the system is inconsistent and has no solutions.
Answer
The system has no solutions.
Often in problems on systems of linear equations there are equations where there are not identical letters, that is, in addition to the letters that denote variables, there are also other letters and they denote some real number. In practice, such equations and systems of equations are led to problems of searching for general properties of any phenomena and objects. That is, have you invented any new material or a device, and to describe its properties, which are common regardless of the size or number of an instance, you need to solve a system of linear equations, where instead of some coefficients for variables there are letters. Let's look at this example.
Using Cramer's formulas, we find:
Answer
And finally, we moved on to the actual complex system equations with four unknowns. The principle of the solution is the same as in the previous examples, but due to the large system it can get confusing. Therefore, let's look at this equation using an example.
In the original determinant, from the elements of the second row we subtracted the elements of the fourth row, and from the elements of the third row we subtracted the elements of the fourth row, which were multiplied by 2. We also subtracted from the elements of the fourth row the elements of the first row, multiplied by two. Transformations of the original determinants at the first three unknown were produced according to the same scheme. Now you can find determinants for unknowns:
To transform the determinant for the fourth unknown, we subtracted the elements of the fourth row from the elements of the first row.
Now using Cramer's formulas you need to find:
Answer
So, we have found the roots of the linear equation system:
Let's sum it up
Using Cramer's method, you can solve systems of linear algebraic equations if the determinant is not equal to zero. This method allows you to find determinants of matrices of the same order as on thanks to Cramer’s formulas when you need to find unknown variables. If all free terms are zero, then their determinants are zero, since they contain a column with zero elements. And of course, if the determinants are equal to zero, it is better to solve the system using the Gaussian method Cramer method in Excel from 2007 (XLSX)
Cramer's method - theorem, examples of solutions updated: November 22, 2019 by: Scientific Articles.Ru
Solving systems of linear algebraic equations (SLAEs) is undoubtedly the most important topic in a linear algebra course. A huge number of problems from all branches of mathematics come down to solving systems of linear equations. These factors explain the reason for this article. The material of the article is selected and structured so that with its help you can
- choose the optimal method for solving your system of linear algebraic equations,
- study the theory of the chosen method,
- solve your system of linear equations by considering detailed solutions to typical examples and problems.
Brief description of the article material.
First let's give everything necessary definitions, concepts and introduce notations.
Next, we will consider methods for solving systems of linear algebraic equations in which the number of equations is equal to the number of unknown variables and which have a unique solution. Firstly, we will focus on Cramer’s method, secondly, we will show the matrix method for solving such systems of equations, and thirdly, we will analyze the Gauss method (the method of sequential elimination of unknown variables). To consolidate the theory, we will definitely solve several SLAEs in different ways.
After this, we will move on to solving systems of linear algebraic equations general view, in which the number of equations does not coincide with the number of unknown variables or the main matrix of the system is singular. Let us formulate the Kronecker-Capelli theorem, which allows us to establish the compatibility of SLAEs. Let us analyze the solution of systems (if they are compatible) using the concept of a basis minor of a matrix. We will also consider the Gauss method and describe in detail the solutions to the examples.
We will definitely dwell on the structure of the general solution of homogeneous and inhomogeneous systems of linear algebraic equations. Let's give the concept fundamental system solutions and show how to write general solution SLAE using vectors of the fundamental solution system. For a better understanding, let's look at a few examples.
In conclusion, we will consider systems of equations that can be reduced to linear ones, as well as various problems in the solution of which SLAEs arise.
Page navigation.
Definitions, concepts, designations.
We will consider systems of p linear algebraic equations with n unknown variables (p can be equal to n) of the form
Unknown variables - coefficients (some real or complex numbers), - free terms (also real or complex numbers).
This form of recording SLAE is called coordinate.
IN matrix form writing this system of equations has the form,
Where 
- the main matrix of the system, - a column matrix of unknown variables, - a column matrix of free terms.
If we add a matrix-column of free terms to matrix A as the (n+1)th column, we get the so-called extended matrix systems of linear equations. Typically, an extended matrix is denoted by the letter T, and the column of free terms is separated by a vertical line from the remaining columns, that is, 
Solving a system of linear algebraic equations called a set of values of unknown variables that turns all equations of the system into identities. The matrix equation for given values of the unknown variables also becomes an identity.
If a system of equations has at least one solution, then it is called joint.
If a system of equations has no solutions, then it is called non-joint.
If a SLAE has a unique solution, then it is called certain; if there is more than one solution, then – uncertain.
If the free terms of all equations of the system are equal to zero 
, then the system is called homogeneous, otherwise – heterogeneous.
Solving elementary systems of linear algebraic equations.
If the number of equations of a system is equal to the number of unknown variables and the determinant of its main matrix is not equal to zero, then such SLAEs will be called elementary. Such systems of equations have a unique solution, and in the case of a homogeneous system, all unknown variables are equal to zero.
We began to study such SLAEs in high school. When solving them, we took one equation, expressed one unknown variable in terms of others and substituted it into the remaining equations, then took the next equation, expressed the next unknown variable and substituted it into other equations, and so on. Or they used the addition method, that is, they added two or more equations to eliminate some unknown variables. We will not dwell on these methods in detail, since they are essentially modifications of the Gauss method.
The main methods for solving elementary systems of linear equations are the Cramer method, the matrix method and the Gauss method. Let's sort them out.
Solving systems of linear equations using Cramer's method.
Suppose we need to solve a system of linear algebraic equations 
in which the number of equations is equal to the number of unknown variables and the determinant of the main matrix of the system is different from zero, that is, .
Let be the determinant of the main matrix of the system, and 
- determinants of matrices that are obtained from A by replacement 1st, 2nd, …, nth column respectively to the column of free members: 
With this notation, unknown variables are calculated using the formulas of Cramer’s method as 
. This is how the solution to a system of linear algebraic equations is found using Cramer's method.
Example.
Cramer's method 
.
Solution.
The main matrix of the system has the form 
. Let's calculate its determinant (if necessary, see the article): 
Since the determinant of the main matrix of the system is nonzero, the system has a unique solution that can be found by Cramer’s method.
Let's compose and calculate the necessary determinants 
(we obtain the determinant by replacing the first column in matrix A with a column of free terms, the determinant by replacing the second column with a column of free terms, and by replacing the third column of matrix A with a column of free terms): 
Finding unknown variables using formulas 
:
Answer:
The main disadvantage of Cramer's method (if it can be called a disadvantage) is the complexity of calculating determinants when the number of equations in the system is more than three.
Solving systems of linear algebraic equations using the matrix method (using an inverse matrix).
Let a system of linear algebraic equations be given in matrix form, where the matrix A has dimension n by n and its determinant is nonzero.
Since , matrix A is invertible, that is, there is an inverse matrix. If we multiply both sides of the equality by the left, we get a formula for finding a matrix-column of unknown variables. This is how we obtained a solution to a system of linear algebraic equations using the matrix method.
Example.
Solve system of linear equations matrix method.
Solution.
Let's rewrite the system of equations in matrix form: 
Because
then the SLAE can be solved using the matrix method. Using the inverse matrix, the solution to this system can be found as 
.
Let's construct an inverse matrix using a matrix from the algebraic complements of the elements of matrix A (if necessary, see the article): 
It remains to calculate the matrix of unknown variables by multiplying the inverse matrix 
to a matrix-column of free members (if necessary, see the article): 
Answer:
or in another notation x 1 = 4, x 2 = 0, x 3 = -1.
The main problem when finding solutions to systems of linear algebraic equations using the matrix method is the complexity of finding the inverse matrix, especially for square matrices of order higher than third.
Solving systems of linear equations using the Gauss method.
Suppose we need to find a solution to a system of n linear equations with n unknown variables 
the determinant of the main matrix of which is different from zero.
The essence of the Gauss method consists of sequentially eliminating unknown variables: first x 1 is excluded from all equations of the system, starting from the second, then x 2 is excluded from all equations, starting from the third, and so on, until only the unknown variable x n remains in the last equation. This process of transforming the equations of a system to sequentially eliminate unknown variables is called direct Gaussian method. After completing the forward stroke of the Gaussian method, x n is found from the last equation, using this value from the penultimate equation, x n-1 is calculated, and so on, x 1 is found from the first equation. The process of calculating unknown variables when moving from the last equation of the system to the first is called inverse of the Gaussian method.
Let us briefly describe the algorithm for eliminating unknown variables.
We will assume that , since we can always achieve this by interchanging the equations of the system. Let's eliminate the unknown variable x 1 from all equations of the system, starting with the second. To do this, to the second equation of the system we add the first, multiplied by , to the third equation we add the first, multiplied by , and so on, to the nth equation we add the first, multiplied by . The system of equations after such transformations will take the form 
where and 
.
We would have arrived at the same result if we had expressed x 1 in terms of other unknown variables in the first equation of the system and substituted the resulting expression into all other equations. Thus, the variable x 1 is excluded from all equations, starting from the second.
Next, we proceed in a similar way, but only with part of the resulting system, which is marked in the figure 
To do this, to the third equation of the system we add the second, multiplied by , to the fourth equation we add the second, multiplied by , and so on, to the nth equation we add the second, multiplied by . The system of equations after such transformations will take the form 
where and 
. Thus, the variable x 2 is excluded from all equations, starting from the third.
Next, we proceed to eliminating the unknown x 3, while we act similarly with the part of the system marked in the figure 
So we continue the direct progression of the Gaussian method until the system takes the form 
From this moment we begin the reverse of the Gaussian method: we calculate x n from the last equation as , using the obtained value of x n we find x n-1 from the penultimate equation, and so on, we find x 1 from the first equation.
Example.
Solve system of linear equations Gauss method.
Solution.
Let us exclude the unknown variable x 1 from the second and third equations of the system. To do this, to both sides of the second and third equations we add the corresponding parts of the first equation, multiplied by and by, respectively: 
Now we eliminate x 2 from the third equation by adding to its left and right sides the left and right sides of the second equation, multiplied by: 
This completes the forward stroke of the Gauss method; we begin the reverse stroke.
From the last equation of the resulting system of equations we find x 3: 
From the second equation we get .
From the first equation we find the remaining unknown variable and thereby complete the reverse of the Gauss method.
Answer:
X 1 = 4, x 2 = 0, x 3 = -1.
Solving systems of linear algebraic equations of general form.
IN general case the number of equations of the system p does not coincide with the number of unknown variables n:
Such SLAEs may have no solutions, have a single solution, or have infinitely many solutions. This statement also applies to systems of equations whose main matrix is square and singular.
Kronecker–Capelli theorem.
Before finding a solution to a system of linear equations, it is necessary to establish its compatibility. The answer to the question when SLAE is compatible and when it is inconsistent is given by Kronecker–Capelli theorem:
In order for a system of p equations with n unknowns (p can be equal to n) to be consistent, it is necessary and sufficient that the rank of the main matrix of the system be equal to the rank of the extended matrix, that is, Rank(A)=Rank(T).
Let us consider, as an example, the application of the Kronecker–Capelli theorem to determine the compatibility of a system of linear equations.
Example.
Find out whether the system of linear equations has 
solutions.
Solution.
. Let's use the method of bordering minors. Minor of the second order 
different from zero. Let's look at the third-order minors bordering it: 
Since all the bordering minors of the third order are equal to zero, the rank of the main matrix is equal to two.
In turn, the rank of the extended matrix 
is equal to three, since the minor is of third order 
different from zero.
Thus, Rang(A), therefore, using the Kronecker–Capelli theorem, we can conclude that the original system of linear equations is inconsistent.
Answer:
The system has no solutions.
So, we have learned to establish the inconsistency of a system using the Kronecker–Capelli theorem.
But how to find a solution to an SLAE if its compatibility is established?
To do this, we need the concept of a basis minor of a matrix and a theorem about the rank of a matrix.
Minor highest order matrix A, different from zero, is called basic.
From the definition of a basis minor it follows that its order is equal to the rank of the matrix. For a non-zero matrix A there can be several basis minors; there is always one basis minor.
For example, consider the matrix 
.
All third-order minors of this matrix are equal to zero, since the elements of the third row of this matrix are the sum of the corresponding elements of the first and second rows.
The following second-order minors are basic, since they are non-zero 
Minors 
are not basic, since they are equal to zero.
Matrix rank theorem.
If the rank of a matrix of order p by n is equal to r, then all row (and column) elements of the matrix that do not form the chosen basis minor are linearly expressed in terms of the corresponding row (and column) elements forming the basis minor.
What does the matrix rank theorem tell us?
If, according to the Kronecker–Capelli theorem, we have established the compatibility of the system, then we choose any basis minor of the main matrix of the system (its order is equal to r), and exclude from the system all equations that do not form the selected basis minor. The SLAE obtained in this way will be equivalent to the original one, since the discarded equations are still redundant (according to the matrix rank theorem, they are a linear combination of the remaining equations).
As a result, after discarding unnecessary equations of the system, two cases are possible.
If the number of equations r in the resulting system is equal to the number of unknown variables, then it will be definite and the only solution can be found by the Cramer method, the matrix method or the Gauss method.
Example.
.
Solution.
Rank of the main matrix of the system 
is equal to two, since the minor is of second order 
different from zero. Extended Matrix Rank 
is also equal to two, since the only third order minor is zero 
and the second-order minor considered above is different from zero. Based on the Kronecker–Capelli theorem, we can assert the compatibility of the original system of linear equations, since Rank(A)=Rank(T)=2.
As a basis minor we take . It is formed by the coefficients of the first and second equations: 
The third equation of the system does not participate in the formation of the basis minor, so we exclude it from the system based on the theorem on the rank of the matrix: 
This is how we obtained an elementary system of linear algebraic equations. Let's solve it using Cramer's method: 
Answer:
x 1 = 1, x 2 = 2.
If the number of equations r in the resulting SLAE less number unknown variables n, then on the left sides of the equations we leave the terms that form the basis minor, and we transfer the remaining terms to the right sides of the equations of the system with the opposite sign.
The unknown variables (r of them) remaining on the left sides of the equations are called main.
Unknown variables (there are n - r pieces) that are on the right sides are called free.
Now we believe that free unknown variables can take arbitrary values, while the r main unknown variables will be expressed through free unknown variables in a unique way. Their expression can be found by solving the resulting SLAE using the Cramer method, the matrix method or the Gauss method.
Let's look at it with an example.
Example.
Solve a system of linear algebraic equations 
.
Solution.
Let's find the rank of the main matrix of the system 
by the method of bordering minors. Let's take a 1 1 = 1 as a non-zero minor of the first order. Let's start searching for a non-zero minor of the second order bordering this minor: 
This is how we found a non-zero minor of the second order. Let's start searching for a non-zero bordering minor of the third order: 
Thus, the rank of the main matrix is three. The rank of the extended matrix is also equal to three, that is, the system is consistent.
We take the found non-zero minor of the third order as the basis one.
For clarity, we show the elements that form the basis minor: 
We leave the terms involved in the basis minor on the left side of the system equations, and transfer the rest with opposite signs to the right sides: 
Let's give the free unknown variables x 2 and x 5 arbitrary values, that is, we accept 
, where are arbitrary numbers. In this case, the SLAE will take the form 
Let us solve the resulting elementary system of linear algebraic equations using Cramer’s method: 
Hence, .
In your answer, do not forget to indicate free unknown variables.
Answer:
Where are arbitrary numbers.
Let's summarize.
To solve a system of general linear algebraic equations, we first determine its compatibility using the Kronecker–Capelli theorem. If the rank of the main matrix is not equal to the rank of the extended matrix, then we conclude that the system is incompatible.
If the rank of the main matrix is equal to the rank of the extended matrix, then we select a basis minor and discard the equations of the system that do not participate in the formation of the selected basis minor.
If the order of the basis minor is equal to the number of unknown variables, then the SLAE has a unique solution, which can be found by any method known to us.
If the order of the basis minor is less than the number of unknown variables, then on the left side of the system equations we leave the terms with the main unknown variables, transfer the remaining terms to the right sides and give arbitrary values to the free unknown variables. From the resulting system of linear equations we find the main unknown variables using the Cramer method, the matrix method or the Gauss method.
Gauss method for solving systems of linear algebraic equations of general form.
The Gauss method can be used to solve systems of linear algebraic equations of any kind without first testing them for compatibility. The process of sequential elimination of unknown variables makes it possible to draw a conclusion about both the compatibility and incompatibility of the SLAE, and if a solution exists, it makes it possible to find it.
From a computational point of view, the Gaussian method is preferable.
Watch it detailed description and analyzed examples in the article the Gauss method for solving systems of linear algebraic equations of general form.
Writing a general solution to homogeneous and inhomogeneous linear algebraic systems using vectors of the fundamental system of solutions.
In this section we will talk about simultaneous homogeneous and inhomogeneous systems of linear algebraic equations that have an infinite number of solutions.
Let us first deal with homogeneous systems.
Fundamental system of solutions homogeneous system of p linear algebraic equations with n unknown variables is a collection of (n – r) linearly independent solutions of this system, where r is the order of the basis minor of the main matrix of the system.
If we denote linearly independent solutions of a homogeneous SLAE as X (1) , X (2) , ..., X (n-r) (X (1) , X (2) , ..., X (n-r) are columnar matrices of dimension n by 1) , then the general solution of this homogeneous system is represented as a linear combination of vectors of the fundamental system of solutions with arbitrary constant coefficients C 1, C 2, ..., C (n-r), that is, .
What does the term general solution of a homogeneous system of linear algebraic equations (oroslau) mean?
The meaning is simple: the formula sets everything possible solutions the original SLAE, in other words, taking any set of values of arbitrary constants C 1, C 2, ..., C (n-r), using the formula we will obtain one of the solutions to the original homogeneous SLAE.
Thus, if we find a fundamental system of solutions, then we can define all solutions of this homogeneous SLAE as .
Let us show the process of constructing a fundamental system of solutions to a homogeneous SLAE.
We select the basis minor of the original system of linear equations, exclude all other equations from the system and transfer all terms containing free unknown variables to the right-hand sides of the equations of the system with opposite signs. Let's give the free unknown variables the values 1,0,0,...,0 and calculate the main unknowns by solving the resulting elementary system of linear equations in any way, for example, using the Cramer method. This will result in X (1) - the first solution of the fundamental system. If we give the free unknowns the values 0,1,0,0,…,0 and calculate the main unknowns, we get X (2) . And so on. If we assign the values 0.0,...,0.1 to the free unknown variables and calculate the main unknowns, we obtain X (n-r) . In this way, a fundamental system of solutions to a homogeneous SLAE will be constructed and its general solution can be written in the form .
For inhomogeneous systems of linear algebraic equations, the general solution is represented in the form , where is the general solution of the corresponding homogeneous system, and is the particular solution of the original inhomogeneous SLAE, which we obtain by giving the free unknowns the values 0,0,…,0 and calculating the values of the main unknowns.
Let's look at examples.
Example.
Find the fundamental system of solutions and the general solution of a homogeneous system of linear algebraic equations 
.
Solution.
The rank of the main matrix of homogeneous systems of linear equations is always equal to the rank of the extended matrix. Let's find the rank of the main matrix using the method of bordering minors. As a non-zero minor of the first order, we take element a 1 1 = 9 of the main matrix of the system. Let's find the bordering non-zero minor of the second order: 
A minor of the second order, different from zero, has been found. Let's go through the third-order minors bordering it in search of a non-zero one: 
All third-order bordering minors are equal to zero, therefore, the rank of the main and extended matrix is equal to two. Let's take . For clarity, let us note the elements of the system that form it: 
The third equation of the original SLAE does not participate in the formation of the basis minor, therefore, it can be excluded: 
We leave the terms containing the main unknowns on the right sides of the equations, and transfer the terms with free unknowns to the right sides:
Let us construct a fundamental system of solutions to the original homogeneous system of linear equations. The fundamental system of solutions of this SLAE consists of two solutions, since the original SLAE contains four unknown variables, and the order of its basis minor is equal to two. To find X (1), we give the free unknown variables the values x 2 = 1, x 4 = 0, then we find the main unknowns from the system of equations 
.
Let's solve it using Cramer's method: 
Thus, .
Now let's construct X (2) . To do this, we give the free unknown variables the values x 2 = 0, x 4 = 1, then we find the main unknowns from the system of linear equations 
.
Let's use Cramer's method again: 
We get.
So we got two vectors of the fundamental system of solutions and , now we can write down the general solution of a homogeneous system of linear algebraic equations: 
, where C 1 and C 2 are arbitrary numbers., are equal to zero. We will also take the minor as a basic one, eliminate the third equation from the system and move the terms with free unknowns to the right-hand sides of the system equations: 
To find, let’s give the free unknown variables the values x 2 = 0 and x 4 = 0, then the system of equations will take the form 
, from where we find the main unknown variables using Cramer’s method: 
We have 
, hence, 
where C 1 and C 2 are arbitrary numbers.
It should be noted that solutions to an indeterminate homogeneous system of linear algebraic equations generate linear space Solution.
The canonical equation of an ellipsoid in a rectangular Cartesian coordinate system has the form 
. Our task is to determine the parameters a, b and c. Since the ellipsoid passes through points A, B and C, then when substituting their coordinates into canonical equation ellipsoid it must turn into an identity. So we get a system of three equations: 
Let's denote 
, then the system will become a system of linear algebraic equations 
.
Let us calculate the determinant of the main matrix of the system: 
Since it is non-zero, we can find the solution using Cramer’s method:
). Obviously, x = 0 and x = 1 are the roots of this polynomial. Quotient from division 
on 
is . Thus, we have an expansion and the original expression takes the form 
.
Let's use the method of indefinite coefficients. 
Equating the corresponding coefficients of the numerators, we arrive at a system of linear algebraic equations 
. Its solution will give us the required uncertain odds A, B, C and D.
Let's solve the system using the Gaussian method: 
Using the reverse of the Gaussian method, we find D = 0, C = -2, B = 1, A = 1.
We get 
Answer:
.
KOSTROMA BRANCH OF THE MILITARY UNIVERSITY OF RCHB PROTECTION
Department of Automation of Troop Control
For teachers only
"I approve"
Head of Department No. 9
Colonel YAKOVLEV A.B.
"____"______________ 2004
Associate Professor A.I. SMIRNOVA
"QUALIFIERS.
SOLUTION OF SYSTEMS OF LINEAR EQUATIONS"
LECTURE No. 2 / 1
Discussed at department meeting No. 9
"____"___________ 2004
Protocol No.___________
Kostroma, 2004.
Introduction
1. Second and third order determinants.
2. Properties of determinants. Decomposition theorem.
3. Cramer's theorem.
Conclusion
Literature
1. V.E. Schneider et al. Short course Higher Mathematics, Volume I, Ch. 2, paragraph 1.
2. V.S. Shchipachev, Higher Mathematics, chapter 10, paragraph 2.
INTRODUCTION
The lecture discusses determinants of the second and third orders and their properties. And also Cramer’s theorem, which allows you to solve systems of linear equations using determinants. Determinants are also used later in the topic "Vector Algebra" when calculating vector product vectors.
1st study question DETERMINANTS OF THE SECOND AND THIRD
ORDER
Consider a table of four numbers of the form
The numbers in the table are indicated by a letter with two indices. The first index indicates the row number, the second the column number.
DEFINITION 1.Second order determinant calledexpressionkind:
(1)Numbers A 11, …, A 22 are called elements of the determinant.
Diagonal formed by elements A 11 ; A 22 is called the main one, and the diagonal formed by the elements A 12 ; A 21 - side by side.
Thus, the second-order determinant is equal to the difference between the products of the elements of the main and secondary diagonals.
Note that the answer is a number.
EXAMPLES. Calculate:
Now consider a table of nine numbers, written in three rows and three columns:
DEFINITION 2. Third order determinant called an expression of the form:
Elements A 11; A 22 ; A 33 – form the main diagonal.
Numbers A 13; A 22 ; A 31 – form a side diagonal.
Let us depict schematically how the plus and minus terms are formed:
" + " " – "The plus includes: the product of the elements on the main diagonal, the remaining two terms are the product of the elements located at the vertices of triangles with bases parallel to the main diagonal.
The minus terms are formed according to the same scheme with respect to the secondary diagonal.
This rule for calculating the third-order determinant is called
Rule T reugolnikov.
EXAMPLES. Calculate using the triangle rule:
COMMENT. Determinants are also called determinants.
2nd study question PROPERTIES OF DETERMINANTS.
EXPANSION THEOREM
Property 1. The value of the determinant will not change if its rows are swapped with the corresponding columns.
.By revealing both determinants, we are convinced of the validity of the equality.
Property 1 establishes the equality of the rows and columns of the determinant. Therefore, we will formulate all further properties of the determinant for both rows and columns.
Property 2. When rearranging two rows (or columns), the determinant changes sign to the opposite one, maintaining absolute value .
.Property 3. Common factor of row elements(or column)can be taken out as a determinant sign.
.Property 4. If the determinant has two identical rows (or columns), then it is equal to zero.
This property can be proven by direct verification, or you can use property 2.
Let us denote the determinant by D. When two identical first and second rows are rearranged, it will not change, but according to the second property it must change sign, i.e.
D = - DÞ 2 D = 0 ÞD = 0.
Property 5. If all elements of a string(or column)are equal to zero, then the determinant is equal to zero.
This property can be considered as special case properties 3 at
Property 6. If the elements of two lines(or columns)the determinants are proportional, then the determinant is equal to zero.
.Can be proven by direct verification or using properties 3 and 4.
Property 7. The value of the determinant will not change if the corresponding elements of another row (or column) are added to the elements of a row (or column), multiplied by the same number.
.Proved by direct verification.
The use of these properties can in some cases facilitate the process of calculating determinants, especially of the third order.
For what follows we will need the concepts of minor and algebraic complement. Let's consider these concepts to define the third order.
DEFINITION 3. Minor of a given element of a third-order determinant is called a second-order determinant obtained from a given element by crossing out the row and column at the intersection of which the given element stands.
Element minor Aij denoted by Mij. So for the element A 11 minor
It is obtained by crossing out the first row and first column in the third-order determinant.
DEFINITION 4. Algebraic complement of the element of the determinant they call it minor multiplied by(-1)k, Wherek- the sum of the row and column numbers at the intersection of which this element stands.
Algebraic complement of an element Aij denoted by Aij.
Thus, Aij =
.Let us write down the algebraic additions for the elements A 11 and A 12.
. .It is useful to remember the rule: the algebraic complement of an element of a determinant is equal to its signed minor plus, if the sum of the row and column numbers in which the element appears is even, and with a sign minus, if this amount odd.
EXAMPLE. Find minors and algebraic complements for the elements of the first row of the determinant:
It is clear that minors and algebraic complements can differ only in sign.
Let us consider without proof an important theorem - determinant expansion theorem.
EXPANSION THEOREM
The determinant is equal to the sum of the products of the elements of any row or column and their algebraic complements.
Using this theorem, we write the expansion of the third-order determinant along the first line.
.In expanded form:
.The last formula can be used as the main one when calculating the third-order determinant.
The expansion theorem allows us to reduce the calculation of the third-order determinant to the calculation of three second-order determinants.
The decomposition theorem provides a second way to calculate third-order determinants.
EXAMPLES. Calculate the determinant using the expansion theorem.
Cramer's method is based on the use of determinants in solving systems of linear equations. This significantly speeds up the solution process.
Cramer's method can be used to solve a system of as many linear equations as there are unknowns in each equation. If the determinant of the system is not equal to zero, then Cramer’s method can be used in the solution, but if it is equal to zero, then it cannot. In addition, Cramer's method can be used to solve systems of linear equations that have a unique solution.
Definition. A determinant made up of coefficients for unknowns is called a determinant of the system and is denoted (delta).
Determinants
are obtained by replacing the coefficients of the corresponding unknowns with free terms:
;
.
Cramer's theorem. If the determinant of the system is nonzero, then the system of linear equations has one unique solution, and the unknown is equal to the ratio of the determinants. The denominator contains the determinant of the system, and the numerator contains the determinant obtained from the determinant of the system by replacing the coefficients of this unknown with free terms. This theorem holds for a system of linear equations of any order.
Example 1. Solve a system of linear equations:
According to Cramer's theorem we have:
So, the solution to system (2):
online calculator, Cramer's solving method.
Three cases when solving systems of linear equations
As is clear from Cramer's theorem, when solving a system of linear equations, three cases can occur:
First case: a system of linear equations has a unique solution
(the system is consistent and definite)
Second case: a system of linear equations has an infinite number of solutions
(the system is consistent and uncertain)
** 
,
those. the coefficients of the unknowns and the free terms are proportional.
Third case: the system of linear equations has no solutions
(the system is inconsistent)
So the system m linear equations with n called variables non-joint, if she does not have a single solution, and joint, if it has at least one solution. A simultaneous system of equations that has only one solution is called certain, and more than one – uncertain.
Examples of solving systems of linear equations using the Cramer method
Let the system be given
.
Based on Cramer's theorem
………….
,
Where 
-
system determinant. We obtain the remaining determinants by replacing the column with the coefficients of the corresponding variable (unknown) with free terms:
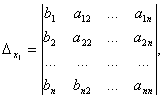
Example 2.
.
Therefore, the system is definite. To find its solution, we calculate the determinants
Using Cramer's formulas we find:
So, (1; 0; -1) is the only solution to the system.
To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.
If in a system of linear equations there are no variables in one or more equations, then in the determinant the corresponding elements are equal to zero! This is the next example.
Example 3. Solve a system of linear equations using the Cramer method:
.
Solution. We find the determinant of the system:
Look carefully at the system of equations and at the determinant of the system and repeat the answer to the question in which cases one or more elements of the determinant are equal to zero. So, the determinant is not equal to zero, therefore the system is definite. To find its solution, we calculate the determinants for the unknowns
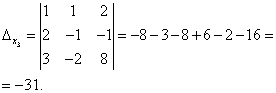
Using Cramer's formulas we find:
So, the solution to the system is (2; -1; 1).
To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.
Top of page
We continue to solve systems using Cramer's method together
As already mentioned, if the determinant of the system is equal to zero, and the determinants of the unknowns are not equal to zero, the system is inconsistent, that is, it has no solutions. Let us illustrate with the following example.
Example 6. Solve a system of linear equations using the Cramer method:
Solution. We find the determinant of the system:
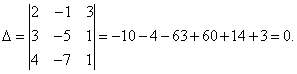
The determinant of the system is equal to zero, therefore, the system of linear equations is either inconsistent and definite, or inconsistent, that is, has no solutions. To clarify, we calculate determinants for unknowns
The determinants of the unknowns are not equal to zero, therefore, the system is inconsistent, that is, it has no solutions.
To check solutions to systems of equations 3 X 3 and 4 X 4, you can use an online calculator using Cramer's solving method.
In problems involving systems of linear equations, there are also those where, in addition to letters denoting variables, there are also other letters. These letters represent a number, most often real. In practice, such equations and systems of equations are led to problems of searching for general properties of any phenomena and objects. That is, you have invented some new material or device, and to describe its properties, which are common regardless of the size or quantity of the specimen, you need to solve a system of linear equations, where instead of some coefficients for variables there are letters. You don't have to look far for examples.
The following example is for a similar problem, only the number of equations, variables, and letters denoting a certain real number increases.
Example 8. Solve a system of linear equations using the Cramer method:
Solution. We find the determinant of the system:
Finding determinants for unknowns
