When adding, degrees are added or multiplied. Degree and its properties

In the previous article we explained what monomials are. In this material we will look at how to solve examples and problems in which they are used. Here we will consider such operations as subtraction, addition, multiplication, division of monomials and raising them to a power with natural indicator. We will show how such operations are defined, outline the basic rules for their implementation and what should be the result. All theoretical concepts, as usual, will be illustrated with examples of problems with descriptions of solutions.

It is most convenient to work with the standard notation of monomials, so we present all expressions that will be used in the article in standard form. If they were originally specified differently, it is recommended to first bring them to a generally accepted form.

Rules for adding and subtracting monomials

Most simple steps that can be done with monomials are subtraction and addition. IN general case the result of these actions will be a polynomial (a monomial is possible in some special cases).

When we add or subtract monomials, we first write down the corresponding sum and difference in the generally accepted form, and then simplify the resulting expression. If there are similar terms, they need to be cited, and the parentheses should be opened. Let's explain with an example.

Example 1

Condition: perform the addition of the monomials − 3 x and 2, 72 x 3 y 5 z.

Solution

Let's write down the sum of the original expressions. Let's add parentheses and put a plus sign between them. We will get the following:

(− 3 x) + (2, 72 x 3 y 5 z)

When we do the parenthesis expansion, we get - 3 x + 2, 72 x 3 y 5 z. This is a polynomial written in standard form, which will be the result of adding these monomials.

Answer:(− 3 x) + (2.72 x 3 y 5 z) = − 3 x + 2.72 x 3 y 5 z.

If we have three, four or more terms, we carry out this action in exactly the same way.

Example 2

Condition: carry out the indicated operations with polynomials in the correct order

3 a 2 - (- 4 a c) + a 2 - 7 a 2 + 4 9 - 2 2 3 a c

Solution

Let's start by opening the brackets.

3 a 2 + 4 a c + a 2 - 7 a 2 + 4 9 - 2 2 3 a c

We see that the resulting expression can be simplified by adding similar terms:

3 a 2 + 4 a c + a 2 - 7 a 2 + 4 9 - 2 2 3 a c = = (3 a 2 + a 2 - 7 a 2) + 4 a c - 2 2 3 a c + 4 9 = = - 3 a 2 + 1 1 3 a c + 4 9

We have a polynomial, which will be the result of this action.

Answer: 3 a 2 - (- 4 a c) + a 2 - 7 a 2 + 4 9 - 2 2 3 a c = - 3 a 2 + 1 1 3 a c + 4 9

In principle, we can add and subtract two monomials, with some restrictions, so that we end up with a monomial. To do this, you need to meet some conditions regarding addends and subtracted monomials. We will tell you how this is done in a separate article.

Rules for multiplying monomials

The multiplication action does not impose any restrictions on the factors. The monomials being multiplied do not have to meet any additional conditions in order for the result to be a monomial.

To perform multiplication of monomials, you need to follow these steps:

Write down the piece correctly.
Expand the parentheses in the resulting expression.
If possible, group factors with the same variables and numeric factors separately.
Perform the necessary operations with numbers and apply the property of multiplication of powers with the same bases to the remaining factors.

Let's see how this is done in practice.

Example 3

Condition: multiply the monomials 2 x 4 y z and - 7 16 t 2 x 2 z 11.

Solution

Let's start by composing the work.

We open the brackets in it and get the following:

2 x 4 y z - 7 16 t 2 x 2 z 11

2 - 7 16 t 2 x 4 x 2 y z 3 z 11

All we have to do is multiply the numbers in the first brackets and apply the property of powers for the second. As a result, we get the following:

2 - 7 16 t 2 x 4 x 2 y z 3 z 11 = - 7 8 t 2 x 4 + 2 y z 3 + 11 = = - 7 8 t 2 x 6 y z 14

Answer: 2 x 4 y z - 7 16 t 2 x 2 z 11 = - 7 8 t 2 x 6 y z 14 .

If our condition contains three or more polynomials, we multiply them using exactly the same algorithm. We will consider the issue of multiplying monomials in more detail in a separate material.

Rules for raising a monomial to a power

We know that a power with a natural exponent is the product of a certain number of identical factors. Their number is indicated by the number in the indicator. According to this definition, raising a monomial to a power is equivalent to multiplying the specified number of identical monomials. Let's see how it's done.

Example 4

Condition: raise the monomial − 2 · a · b 4 to the power 3 .

Solution

We can replace exponentiation with multiplication of 3 monomials − 2 · a · b 4 . Let's write it down and get the desired answer:

(− 2 · a · b 4) 3 = (− 2 · a · b 4) · (− 2 · a · b 4) · (− 2 · a · b 4) = = ((− 2) · (− 2) · (− 2)) · (a · a · a) · (b 4 · b 4 · b 4) = − 8 · a 3 · b 12

Answer:(− 2 · a · b 4) 3 = − 8 · a 3 · b 12 .

But what if the degree has a large indicator? It is inconvenient to record a large number of factors. Then, to solve such a problem, we need to apply the properties of a degree, namely the property of a product degree and the property of a degree in a degree.

Let's solve the problem we presented above using the indicated method.

Example 5

Condition: raise − 2 · a · b 4 to the third power.

Solution

Knowing the power-to-degree property, we can proceed to an expression of the following form:

(− 2 · a · b 4) 3 = (− 2) 3 · a 3 · (b 4) 3 .

After this, we raise to the power - 2 and apply the property of powers to powers:

(− 2) 3 · (a) 3 · (b 4) 3 = − 8 · a 3 · b 4 · 3 = − 8 · a 3 · b 12 .

Answer:− 2 · a · b 4 = − 8 · a 3 · b 12 .

We also devoted a separate article to raising a monomial to a power.

Rules for dividing monomials

The last action with monomials, which we will analyze in this material, – division of a monomial by a monomial. As a result, we should obtain a rational (algebraic) fraction (in some cases it is possible to obtain a monomial). Let us immediately clarify that division by zero monomial is not defined, since division by 0 is not defined.

To perform division, we need to write down the indicated monomials in the form of a fraction and reduce it, if possible.

Example 6

Condition: divide the monomial − 9 · x 4 · y 3 · z 7 by − 6 · p 3 · t 5 · x 2 · y 2 .

Solution

Let's start by writing monomials in fraction form.

9 x 4 y 3 z 7 - 6 p 3 t 5 x 2 y 2

This fraction can be reduced. After performing this action we get:

3 x 2 y z 7 2 p 3 t 5

Answer:- 9 x 4 y 3 z 7 - 6 p 3 t 5 x 2 y 2 = 3 x 2 y z 7 2 p 3 t 5 .

The conditions under which, as a result of dividing monomials, we obtain a monomial, are given in a separate article.

If you notice an error in the text, please highlight it and press Ctrl+Enter

How to multiply powers? Which powers can be multiplied and which cannot? How to multiply a number by a power?

In algebra, you can find a product of powers in two cases:

1) if the degrees have the same bases;

2) if the degrees have the same indicators.

When multiplying powers with the same bases, the base must be left the same, and the exponents must be added:

When multiplying powers with the same exponents general indicator can be taken out of brackets:

Let's look at how to multiply powers by specific examples.

The unit is not written in the exponent, but when multiplying powers, they take into account:

When multiplying, there can be any number of powers. It should be remembered that you don’t have to write the multiplication sign before the letter:

In expressions, exponentiation is done first.

If you need to multiply a number by a power, you should first perform the exponentiation, and only then the multiplication:

www.algebraclass.ru

Addition, subtraction, multiplication, and division of powers

Addition and subtraction of powers

It is obvious that numbers with powers can be added like other quantities , by adding them one after another with their signs.

So, the sum of a 3 and b 2 is a 3 + b 2.
The sum of a 3 - b n and h 5 -d 4 is a 3 - b n + h 5 - d 4.

Odds equal degrees of identical variables can be added or subtracted.

So, the sum of 2a 2 and 3a 2 is equal to 5a 2.

It is also obvious that if you take two squares a, or three squares a, or five squares a.

But degrees various variables And various degrees identical variables, must be composed by adding them with their signs.

So, the sum of a 2 and a 3 is the sum of a 2 + a 3.

It is obvious that the square of a, and the cube of a, is not equal to twice the square of a, but to twice the cube of a.

The sum of a 3 b n and 3a 5 b 6 is a 3 b n + 3a 5 b 6.

Subtraction powers are carried out in the same way as addition, except that the signs of the subtrahends must be changed accordingly.

Or:
2a 4 - (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a - h) 6 - 2(a - h) 6 = 3(a - h) 6

Multiplying powers

Numbers with powers can be multiplied, like other quantities, by writing them one after the other, with or without a multiplication sign between them.

Thus, the result of multiplying a 3 by b 2 is a 3 b 2 or aaabb.

Or:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

The result in the last example can be ordered by adding identical variables.
The expression will take the form: a 5 b 5 y 3.

By comparing several numbers (variables) with powers, we can see that if any two of them are multiplied, then the result is a number (variable) with a power equal to amount degrees of terms.

So, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Here 5 is the power of the multiplication result, which is equal to 2 + 3, the sum of the powers of the terms.

So, a n .a m = a m+n .

For a n , a is taken as a factor as many times as the power of n;

And a m is taken as a factor as many times as the degree m is equal to;

That's why, powers with the same bases can be multiplied by adding the exponents of the powers.

So, a 2 .a 6 = a 2+6 = a 8 . And x 3 .x 2 .x = x 3+2+1 = x 6 .

Or:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h - y) n ⋅ (b + h - y) = (b + h - y) n+1

Multiply (x 3 + x 2 y + xy 2 + y 3) ⋅ (x - y).
Answer: x 4 - y 4.
Multiply (x 3 + x – 5) ⋅ (2x 3 + x + 1).

This rule is also true for numbers whose exponents are negative.

1. So, a -2 .a -3 = a -5 . This can be written as (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

If a + b are multiplied by a - b, the result will be a 2 - b 2: that is

The result of multiplying the sum or difference of two numbers is equal to the sum or difference of their squares.

If you multiply the sum and difference of two numbers raised to square, the result will be equal to the sum or difference of these numbers in fourth degrees.

So, (a - y).(a + y) = a 2 - y 2.
(a 2 - y 2)⋅(a 2 + y 2) = a 4 - y 4.
(a 4 - y 4)⋅(a 4 + y 4) = a 8 - y 8.

Division of degrees

Numbers with powers can be divided like other numbers, by subtracting from the dividend, or by placing them in fraction form.

Thus, a 3 b 2 divided by b 2 is equal to a 3.

Writing a 5 divided by a 3 looks like $\frac $. But this is equal to a 2 . In a series of numbers
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
any number can be divided by another, and the exponent will be equal to difference indicators of divisible numbers.

When dividing degrees with the same base, their exponents are subtracted..

So, y 3:y 2 = y 3-2 = y 1. That is, $\frac = y$.

And a n+1:a = a n+1-1 = a n . That is, $\frac = a^n$.

Or:
y 2m: y m = y m
8a n+m: 4a m = 2a n
12(b + y) n: 3(b + y) 3 = 4(b +y) n-3

The rule is also true for numbers with negative values of degrees.
The result of dividing a -5 by a -3 is a -2.
Also, $\frac: \frac = \frac .\frac = \frac = \frac $.

h 2:h -1 = h 2+1 = h 3 or $h^2:\frac = h^2.\frac = h^3$

It is necessary to master multiplication and division of powers very well, since such operations are very widely used in algebra.

Examples of solving examples with fractions containing numbers with powers

1. Decrease the exponents by $\frac $ Answer: $\frac $.

2. Decrease exponents by $\frac$. Answer: $\frac$ or 2x.

3. Reduce the exponents a 2 /a 3 and a -3 /a -4 and bring to a common denominator.
a 2 .a -4 is a -2 the first numerator.
a 3 .a -3 is a 0 = 1, the second numerator.
a 3 .a -4 is a -1 , the common numerator.
After simplification: a -2 /a -1 and 1/a -1 .

4. Reduce the exponents 2a 4 /5a 3 and 2 /a 4 and bring to a common denominator.
Answer: 2a 3 /5a 7 and 5a 5 /5a 7 or 2a 3 /5a 2 and 5/5a 2.

5. Multiply (a 3 + b)/b 4 by (a - b)/3.

6. Multiply (a 5 + 1)/x 2 by (b 2 - 1)/(x + a).

7. Multiply b 4 /a -2 by h -3 /x and a n /y -3 .

8. Divide a 4 /y 3 by a 3 /y 2 . Answer: a/y.

Properties of degree

We remind you that in this lesson we will understand properties of degrees with natural indicators and zero. Powers with rational exponents and their properties will be discussed in lessons for 8th grade.

A power with a natural exponent has several important properties that allow us to simplify calculations in examples with powers.

Property No. 1
Product of powers

When multiplying powers with the same bases, the base remains unchanged, and the exponents of the powers are added.

a m · a n = a m + n, where “a” is any number, and “m”, “n” are any natural numbers.

This property of powers also applies to the product of three or more powers.

Simplify the expression.
b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15

Present it as a degree.
6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17

Present it as a degree.
(0.8) 3 · (0.8) 12 = (0.8) 3 + 12 = (0.8) 15

Please note that in the specified property we were talking only about the multiplication of powers with the same bases. It does not apply to their addition.

You cannot replace the sum (3 3 + 3 2) with 3 5. This is understandable if
calculate (3 3 + 3 2) = (27 + 9) = 36, and 3 5 = 243

Property No. 2
Partial degrees

When dividing powers with the same base, the base remains unchanged, and the exponent of the divisor is subtracted from the exponent of the dividend.

Write the quotient as a power
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2

Calculate.

11 3 − 2 4 2 − 1 = 11 4 = 44
Example. Solve the equation. We use the property of quotient powers.
3 8: t = 3 4

Answer: t = 3 4 = 81

Using properties No. 1 and No. 2, you can easily simplify expressions and perform calculations.

Example. Find the value of an expression using the properties of exponents.

2 11 − 5 = 2 6 = 64

Please note that in Property 2 we were only talking about dividing powers with the same bases.

You cannot replace the difference (4 3 −4 2) with 4 1. This is understandable if you calculate (4 3 −4 2) = (64 − 16) = 48, and 4 1 = 4

Property No. 3
Raising a degree to a power

When raising a degree to a power, the base of the degree remains unchanged, and the exponents are multiplied.

(a n) m = a n · m, where “a” is any number, and “m”, “n” are any natural numbers.

Please note that property No. 4, like other properties of degrees, is also applied in reverse order.

(a n · b n)= (a · b) n

That is, to multiply powers with the same exponents, you can multiply the bases, but leave the exponent unchanged.

Example. Calculate.
2 4 5 4 = (2 5) 4 = 10 4 = 10,000

Example. Calculate.
0.5 16 2 16 = (0.5 2) 16 = 1

In more complex examples There may be cases when multiplication and division must be performed over powers with different bases and different indicators. In this case, we advise you to do the following.

For example, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216

An example of raising a decimal to a power.

4 21 (−0.25) 20 = 4 4 20 (−0.25) 20 = 4 (4 (−0.25)) 20 = 4 (−1) 20 = 4 1 = 4

Properties 5
Power of a quotient (fraction)

To raise a quotient to a power, you can raise the dividend and the divisor separately to this power, and divide the first result by the second.

(a: b) n = a n: b n, where “a”, “b” are any rational numbers, b ≠ 0, n - any natural number.

Example. Present the expression as a quotient of powers.
(5: 3) 12 = 5 12: 3 12

We remind you that a quotient can be represented as a fraction. Therefore, we will dwell on the topic of raising a fraction to a power in more detail on the next page.

Powers and roots

Operations with powers and roots. Degree with negative ,

zero and fractional indicator. About expressions that have no meaning.

Operations with degrees.

1. When multiplying powers with the same base, their exponents are added:

a m · a n = a m + n .

2. When dividing degrees with the same base, their exponents are deducted .

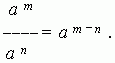
3. The degree of the product of two or more factors is equal to the product of the degrees of these factors.

4. The degree of a ratio (fraction) is equal to the ratio of the degrees of the dividend (numerator) and divisor (denominator):

(a/b) n = a n / b n .

5. When raising a power to a power, their exponents are multiplied:

All the above formulas are read and executed in both directions from left to right and vice versa.

EXAMPLE (2 3 5 / 15)² = 2² · 3² · 5² / 15² = 900 / 225 = 4 .

Operations with roots. In all the formulas below, the symbol means arithmetic root(the radical expression is positive).

1. The root of the product of several factors is equal to the product of the roots of these factors:

2. The root of a ratio is equal to the ratio of the roots of the dividend and the divisor:

3. When raising a root to a power, it is enough to raise to this power radical number:

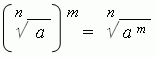
4. If you increase the degree of the root by m times and at the same time raise the radical number to the mth power, then the value of the root will not change:

5. If you reduce the degree of the root by m times and simultaneously extract the mth root of the radical number, then the value of the root will not change:

Expanding the concept of degree. So far we have considered degrees only with natural exponents; but operations with powers and roots can also lead to negative, zero And fractional indicators. All these exponents require additional definition.

A degree with a negative exponent. The power of a certain number with a negative (integer) exponent is defined as one divided by the power of the same number with an exponent equal to the absolute value of the negative exponent:

Now the formula a m : a n = a m - n can be used not only for m, more than n, but also with m, less than n .

EXAMPLE a 4: a 7 = a 4 — 7 = a — 3 .

If we want the formula a m : a n = a m — n was fair when m = n, we need a definition of degree zero.

A degree with a zero index. The power of any non-zero number with exponent zero is 1.

EXAMPLES. 2 0 = 1, ( – 5) 0 = 1, (– 3 / 5) 0 = 1.

Degree with a fractional exponent. In order to raise a real number a to the power m / n, you need to extract the nth root of the mth power of this number a:

About expressions that have no meaning. There are several such expressions.

Where a ≠ 0 , does not exist.

In fact, if we assume that x is a certain number, then in accordance with the definition of the division operation we have: a = 0· x, i.e. a= 0, which contradicts the condition: a ≠ 0

— any number.

In fact, if we assume that this expression is equal to some number x, then according to the definition of the division operation we have: 0 = 0 · x. But this equality takes place when any number x, which was what needed to be proven.

0 0 — any number.

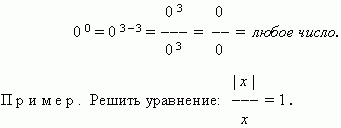
Solution. Let's consider three main cases:

1) x = 0 – this value does not satisfy this equation

2) when x> 0 we get: x/x= 1, i.e. 1 = 1, which means

What x– any number; but taking into account that in

in our case x> 0, the answer is x > 0 ;

Rules for multiplying powers with different bases

DEGREE WITH RATIONAL INDICATOR,

POWER FUNCTION IV

§ 69. Multiplication and division of powers with the same bases

Theorem 1. To multiply powers with the same bases, it is enough to add the exponents and leave the base the same, that is

Proof. By definition of degree

2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.

We looked at the product of two powers. In fact, the proven property is true for any number of powers with the same bases.

Theorem 2. To divide powers with the same bases, when the index of the dividend is greater than the index of the divisor, it is enough to subtract the index of the divisor from the index of the dividend, and leave the base the same, that is at t > p

(a =/= 0)

Proof. Recall that the quotient of dividing one number by another is the number that, when multiplied by the divisor, gives the dividend. Therefore, prove the formula where a =/= 0, it's the same as proving the formula

If t > p , then the number t - p will be natural; therefore, by Theorem 1

Theorem 2 is proven.

It should be noted that the formula

we have proved it only under the assumption that t > p . Therefore, from what has been proven, it is not yet possible to draw, for example, the following conclusions:

In addition, we have not yet considered degrees with negative exponents and we do not yet know what meaning can be given to expression 3 - 2 .

Theorem 3. To raise a degree to a power, it is enough to multiply the exponents, leaving the base of the degree the same, that is

Proof. Using the definition of degree and Theorem 1 of this section, we obtain:

Q.E.D.

For example, (2 3) 2 = 2 6 = 64;

518 (Oral) Determine X from the equations:

1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;

2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .

519. (Set no.) Simplify:

520. (Set no.) Simplify:

521. Present these expressions in the form of degrees with the same bases:

1) 32 and 64; 3) 8 5 and 16 3; 5) 4 100 and 32 50;

2) -1000 and 100; 4) -27 and -243; 6) 81 75 8 200 and 3 600 4 150.

If we ignore the eighth power, what do we see here? Let's remember the 7th grade program. So, do you remember? This is the formula for abbreviated multiplication, namely the difference of squares! We get:

Let's look carefully at the denominator. It looks a lot like one of the numerator factors, but what's wrong? The order of the terms is wrong. If they were reversed, the rule could apply.

But how to do this? It turns out that it’s very easy: the even degree of the denominator helps us here.

Magically the terms changed places. This “phenomenon” applies to any expression to an even degree: we can easily change the signs in parentheses.

But it's important to remember: all signs change at the same time!

Let's go back to the example:

And again the formula:

Whole we call the natural numbers, their opposites (that is, taken with the " " sign) and the number.

positive integer, and it is no different from natural, then everything looks exactly like in the previous section.

Now let's look at new cases. Let's start with an indicator equal to.

Any number to the zero power is equal to one:

As always, let us ask ourselves: why is this so?

Let's consider some degree with a base. Take, for example, and multiply by:

So, we multiplied the number by, and we got the same thing as it was - . What number should you multiply by so that nothing changes? That's right, on. Means.

We can do the same with an arbitrary number:

Let's repeat the rule:

Any number to the zero power is equal to one.

But there are exceptions to many rules. And here it is also there - this is a number (as a base).

On the one hand, it must be equal to any degree - no matter how much you multiply zero by itself, you will still get zero, this is clear. But on the other hand, like any number to the zero power, it must be equal. So how much of this is true? The mathematicians decided not to get involved and refused to raise zero to the zero power. That is, now we cannot not only divide by zero, but also raise it to the zero power.

Let's move on. In addition to natural numbers and numbers, integers also include negative numbers. To understand what a negative power is, let’s do as last time: multiply some normal number by the same number to a negative power:

From here it’s easy to express what you’re looking for:

Now let’s extend the resulting rule to an arbitrary degree:

So, let's formulate a rule:

A number with a negative power is the reciprocal of the same number with a positive power. But at the same time The base cannot be null:(because you can’t divide by).

Let's summarize:

I. The expression is not defined in the case. If, then.

II. Any number to the zero power is equal to one: .

III. Number, not equal to zero, to a negative degree is the inverse of the same number to a positive degree: .

Tasks for independent solution:

Well, as usual, examples for independent solutions:

Analysis of problems for independent solution:

I know, I know, the numbers are scary, but on the Unified State Exam you have to be prepared for anything! Solve these examples or analyze their solutions if you couldn’t solve them and you will learn to cope with them easily in the exam!

Let's continue to expand the range of numbers “suitable” as an exponent.

Now let's consider rational numbers. What numbers are called rational?

Answer: everything that can be represented as a fraction, where and are integers, and.

To understand what it is "fractional degree", consider the fraction:

Let's raise both sides of the equation to a power:

Now let's remember the rule about "degree to degree":

What number must be raised to a power to get?

This formulation is the definition of the root of the th degree.

Let me remind you: the root of the th power of a number () is a number that, when raised to a power, is equal to.

That is, the root of the th power is the inverse operation of raising to a power: .

It turns out that. Obviously this special case can be expanded: .

Now we add the numerator: what is it? The answer is easy to obtain using the power-to-power rule:

But can the base be any number? After all, the root cannot be extracted from all numbers.

None!

Let us remember the rule: any number raised to an even power is a positive number. That is, it is impossible to extract even roots from negative numbers!

This means that such numbers cannot be raised to a fractional power with an even denominator, that is, the expression does not make sense.

What about the expression?

But here a problem arises.

The number can be represented in the form of other, reducible fractions, for example, or.

And it turns out that it exists, but does not exist, but these are just two different records of the same number.

Or another example: once, then you can write it down. But if we write down the indicator differently, we will again get into trouble: (that is, we got a completely different result!).

To avoid such paradoxes, we consider only positive base exponent with fractional exponent.

So if:

— natural number;
- integer;

Examples:

Rational exponents are very useful for transforming expressions with roots, for example:

5 examples to practice

Analysis of 5 examples for training

1. Don't forget about the usual properties of degrees:

2. . Here we remember that we forgot to learn the table of degrees:

after all - this is or. The solution is found automatically: .

Well, now comes the hardest part. Now we'll figure it out degree with irrational exponent.

All the rules and properties of degrees here are exactly the same as for a degree with a rational exponent, with the exception

After all, by definition, irrational numbers are numbers that cannot be represented as a fraction, where and are integers (that is, irrational numbers are all real numbers except rational ones).

When studying degrees with natural, integer and rational exponents, each time we created a certain “image”, “analogy”, or description in more familiar terms.

For example, a degree with a natural exponent is a number multiplied by itself several times;

...number to the zeroth power- this is, as it were, a number multiplied by itself once, that is, they have not yet begun to multiply it, which means that the number itself has not even appeared yet - therefore the result is only a certain “blank number”, namely a number;

...negative integer degree- it’s as if something happened “ reverse process", that is, the number was not multiplied by itself, but divided.

By the way, in science a degree with a complex exponent is often used, that is, the exponent is not even a real number.

But at school we don’t think about such difficulties; you will have the opportunity to comprehend these new concepts at the institute.

WHERE WE ARE SURE YOU WILL GO! (if you learn to solve such examples :))

For example:

Decide for yourself:

Analysis of solutions:

1. Let's start with the usual rule for raising a power to a power:

Now look at the indicator. Doesn't he remind you of anything? Let us recall the formula for abbreviated multiplication of difference of squares:

In this case,

It turns out that:

Answer: .

2. We reduce fractions in exponents to the same form: either both decimals or both ordinary ones. We get, for example:

Answer: 16

3. Nothing special, we use the usual properties of degrees:

ADVANCED LEVEL

Determination of degree

A degree is an expression of the form: , where:

— degree basis;
- exponent.

Degree with natural indicator (n = 1, 2, 3,...)

Raising a number to the natural power n means multiplying the number by itself times:

Degree with an integer exponent (0, ±1, ±2,...)

If the exponent is positive integer number:

Construction to the zero degree:

The expression is indefinite, because, on the one hand, to any degree is this, and on the other hand, any number to the th degree is this.

If the exponent is negative integer number:

(because you can’t divide by).

Once again about zeros: the expression is not defined in the case. If, then.

Examples:

Power with rational exponent

— natural number;
- integer;

Examples:

Properties of degrees

To make it easier to solve problems, let’s try to understand: where did these properties come from? Let's prove them.

Let's see: what is and?

By definition:

So, on the right side of this expression we get the following product:

But by definition it is a power of a number with an exponent, that is:

Q.E.D.

Example : Simplify the expression.

Solution : .

Example : Simplify the expression.

Solution : It is important to note that in our rule Necessarily there must be the same reasons. Therefore, we combine the powers with the base, but it remains a separate factor:

Another important note: this rule - only for product of powers!

Under no circumstances can you write that.

Just as with the previous property, let us turn to the definition of degree:

Let's regroup this work like this:

It turns out that the expression is multiplied by itself times, that is, according to the definition, this is the th power of the number:

In essence, this can be called “taking the indicator out of brackets.” But you can never do this in total: !

Let's remember the abbreviated multiplication formulas: how many times did we want to write? But this is not true, after all.

Power with a negative base.

Up to this point we have only discussed what it should be like indicator degrees. But what should be the basis? In powers of natural indicator the basis may be any number .

Indeed, we can multiply any numbers by each other, be they positive, negative, or even. Let's think about which signs ("" or "") will have degrees of positive and negative numbers?

For example, is the number positive or negative? A? ?

With the first one, everything is clear: no matter how many positive numbers we multiply by each other, the result will be positive.

But the negative ones are a little more interesting. We remember the simple rule from 6th grade: “minus for minus gives a plus.” That is, or. But if we multiply by (), we get - .

And so on ad infinitum: with each subsequent multiplication the sign will change. We can formulate the following simple rules:

even degree, - number positive.
Negative number raised to odd degree, - number negative.
A positive number to any degree is a positive number.
Zero to any power is equal to zero.

Determine for yourself what sign the following expressions will have:

1.	2.	3.
4.	5.	6.

Did you manage? Here are the answers:

1) ; 2) ; 3) ; 4) ; 5) ; 6) .

In the first four examples, I hope everything is clear? We simply look at the base and exponent and apply the appropriate rule.

In example 5) everything is also not as scary as it seems: after all, it doesn’t matter what the base is equal to - the degree is even, which means the result will always be positive. Well, except when the base is zero. The base is not equal, is it? Obviously not, since (because).

Example 6) is no longer so simple. Here you need to find out which is less: or? If we remember that, it becomes clear that, which means the base is less than zero. That is, we apply rule 2: the result will be negative.

And again we use the definition of degree:

Everything is as usual - we write down the definition of degrees and divide them by each other, divide them into pairs and get:

Before we look at the last rule, let's solve a few examples.

Calculate the expressions:

Solutions :

If we ignore the eighth power, what do we see here? Let's remember the 7th grade program. So, do you remember? This is the formula for abbreviated multiplication, namely the difference of squares!

We get:

Let's look carefully at the denominator. It looks a lot like one of the numerator factors, but what's wrong? The order of the terms is wrong. If they were reversed, rule 3 could apply. But how? It turns out that it’s very easy: the even degree of the denominator helps us here.

If you multiply it by, nothing changes, right? But now it turns out like this:

Magically the terms changed places. This “phenomenon” applies to any expression to an even degree: we can easily change the signs in parentheses. But it's important to remember: All signs change at the same time! You can’t replace it with by changing only one disadvantage we don’t like!

Let's go back to the example:

And again the formula:

So now the last rule:

How will we prove it? Of course, as usual: let’s expand on the concept of degree and simplify it:

Well, now let's open the brackets. How many letters are there in total? times by multipliers - what does this remind you of? This is nothing more than a definition of an operation multiplication: There were only multipliers there. That is, this, by definition, is a power of a number with an exponent:

Example:

Degree with irrational exponent

In addition to information about degrees for the average level, we will analyze the degree with an irrational exponent. All the rules and properties of degrees here are exactly the same as for a degree with a rational exponent, with the exception - after all, by definition, irrational numbers are numbers that cannot be represented as a fraction, where and are integers (that is, irrational numbers are all real numbers except rational numbers).

When studying degrees with natural, integer and rational exponents, each time we created a certain “image”, “analogy”, or description in more familiar terms. For example, a degree with a natural exponent is a number multiplied by itself several times; a number to the zero power is, as it were, a number multiplied by itself times, that is, they have not yet begun to multiply it, which means that the number itself has not even appeared yet - therefore the result is only a certain “blank number”, namely a number; a degree with an integer negative exponent - it’s as if some “reverse process” had occurred, that is, the number was not multiplied by itself, but divided.

It is extremely difficult to imagine a degree with an irrational exponent (just as it is difficult to imagine a 4-dimensional space). It is rather a purely mathematical object that mathematicians created to extend the concept of degree to the entire space of numbers.

By the way, in science a degree with a complex exponent is often used, that is, the exponent is not even a real number. But at school we don’t think about such difficulties; you will have the opportunity to comprehend these new concepts at the institute.

So what do we do if we see an irrational exponent? We are trying our best to get rid of it! :)

For example:

Decide for yourself:

Answers:

Let's remember the difference of squares formula. Answer: .
We reduce the fractions to the same form: either both decimals or both ordinary ones. We get, for example: .
Nothing special, we use the usual properties of degrees:

SUMMARY OF THE SECTION AND BASIC FORMULAS

Degree called an expression of the form: , where:

Degree with an integer exponent

a degree whose exponent is a natural number (i.e., integer and positive).

Power with rational exponent

degree, the exponent of which is negative and fractional numbers.

Degree with irrational exponent

a degree whose exponent is an infinite decimal fraction or root.

Properties of degrees

Features of degrees.

Negative number raised to even degree, - number positive.
Negative number raised to odd degree, - number negative.
A positive number to any degree is a positive number.
Zero is equal to any power.
Any number to the zero power is equal.

NOW YOU HAVE THE WORD...

How do you like the article? Write below in the comments whether you liked it or not.

Tell us about your experience using degree properties.

Perhaps you have questions. Or suggestions.

Write in the comments.

And good luck on your exams!

Articles on science and mathematics

Properties of powers with the same bases

There are three properties of degrees with the same bases and natural exponents. This

Work sum

Private two powers with the same bases is equal to the expression where the base is the same and the exponent is difference indicators of the original factors.

Raising a number to a power is equal to an expression in which the base is the same number and the exponent is work two degrees.

Be careful! Rules regarding addition and subtraction degrees with the same bases doesn't exist.

Let us write these properties-rules in the form of formulas:

a m × a n = a m+n

a m ÷ a n = a m–n

(a m) n = a mn

Now let's look at them using specific examples and try to prove them.

5 2 × 5 3 = 5 5 - here we applied the rule; Now let’s imagine how we would solve this example if we didn’t know the rules:

5 2 × 5 3 = 5 × 5 × 5 × 5 × 5 = 5 5 - five squared is five times five, and cubed is the product of three fives. The result is the product of five fives, but this is something other than five to the fifth power: 5 5 .

3 9 ÷ 3 5 = 3 9–5 = 3 4. Let's write the division as a fraction:

It can be shortened:

As a result we get:

Thus, we proved that when dividing two powers with the same bases, their exponents must be subtracted.

However, when dividing, the divisor cannot be equal to zero (since you cannot divide by zero). In addition, since we consider degrees only with natural exponents, we cannot, as a result of subtracting exponents, obtain a number less than 1. Therefore, restrictions are imposed on the formula a m ÷ a n = a m–n: a ≠ 0 and m > n.

Let's move on to the third property:
(2 2) 4 = 2 2×4 = 2 8

Let's write it in expanded form:
(2 2) 4 = (2 × 2) 4 = (2 × 2) × (2 × 2) × (2 × 2) × (2 × 2) = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 2 8

You can come to this conclusion by reasoning logically. You need to multiply two squared four times. But there are two twos in each square, which means there will be eight twos in total.

scienceland.info