Как определить положение центра тяжести тела. Определение координат центра тяжести плоских фигур

– вычислению центра тяжести плоской ограниченной фигуры . Многие читатели интуитивно понимают, что такое центр тяжести, но, тем не менее, рекомендую повторить материал одного из уроков аналитической геометрии , где я разобрал задачу о центре тяжести треугольника и в доступной форме расшифровал физический смысл этого термина.

В самостоятельных и контрольных заданиях для решения, как правило, предлагается простейший случай – плоская ограниченная однородная фигура, то есть фигура постоянной физической плотности – стеклянная, деревянная, оловянная чугунные игрушки, тяжёлое детство и т.д. Далее по умолчанию речь пойдёт только о таких фигурах =)

Первое правило и простейший пример : если у плоской фигуры есть центр симметрии , то он является центром тяжести данной фигуры . Например, центр круглой однородной пластины. Логично и по-житейски понятно – масса такой фигуры «справедливо распределена во все стороны» относительно центра. Верти – не хочу.

Однако в суровых реалиях вам вряд ли подкинут сладкую эллиптическую шоколадку , поэтому придётся вооружиться серьёзным кухонным инструментом:

Координаты центра тяжести плоской однородной ограниченной фигуры рассчитываются по следующим формулам :

, или :

, где – площадь области (фигуры); или совсем коротко :

, где

Интеграл будем условно называть «иксовым» интегралом, а интеграл – «игрековым» интегралом.

Примечание-справка : для плоской ограниченной неоднородной фигуры, плотность которой задана функцией , формулы более сложные:
, где – масса фигуры; в случае однородной плотности они упрощаются до вышеприведённых формул.

На формулах, собственно, вся новизна и заканчивается, остальное – это ваше умение решать двойные интегралы , кстати, сейчас предоставляется прекрасная возможность потренироваться и усовершенствовать свою технику. А совершенству, как известно, нет предела =)

Закинемся бодрящей порцией парабол:

Пример 1

Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями .

Решение : линии здесь элементарны: задаёт ось абсцисс, а уравнение – параболу, которая легко и быстро строится с помощью геометрических преобразований графиков :

– парабола , сдвинутая на 2 единицы влево и на 1 единицу вниз.

Я выполню сразу весь чертёж с готовой точкой центра тяжести фигуры:

Правило второе : если у фигуры существует ось симметрии , то центр тяжести данной фигуры обязательно лежит на этой оси .

В нашем случае фигура симметрична относительно прямой , то есть фактически мы уже знаем «иксовую» координату точки «эм».

Также обратите внимание, что по вертикали центр тяжести смещён ближе к оси абсцисс, поскольку там фигура более массивна.

Да, возможно, ещё не все до конца поняли, что такое центр тяжести: пожалуйста, поднимите вверх указательный палец и мысленно поставьте на него заштрихованную «подошву» точкой . Теоретически фигура не должна упасть.

Координаты центра тяжести фигуры найдём по формулам , где .

Порядок обхода области (фигуры) здесь очевиден:

Внимание! Определяемся с наиболее выгодным порядком обхода один раз – и используем его для всех интегралов!

1) Сначала вычислим площадь фигуры. Ввиду относительной простоты интеграла решение можно оформить компактно, главное, не запутаться в вычислениях:

Смотрим на чертёж и прикидываем по клеточкам площадь. Получилось около дела.

2) Иксовая координата центра тяжести уже найдена «графическим методом», поэтому можно сослаться на симметрию и перейти к следующему пункту. Однако так делать всё-таки не советую – велика вероятность, что решение забракуют с формулировкой «используйте формулу».

Заметьте, что здесь можно обойтись исключительно устными вычислениями – иногда совсем не обязательно приводить дроби к общему знаменателю или мучить калькулятор.

Таким образом:
, что и требовалось получить.

3) Найдём ординату центра тяжести. Вычислим «игрековый» интеграл:

А вот тут без калькулятора пришлось бы тяжко. На всякий случай закомментирую, что в результате умножения многочленов получается 9 членов, причём некоторые из них подобны. Подобные слагаемые я привёл устно (как это обычно принято делать в похожих случаях) и сразу записал итоговую сумму .

В результате:
, что очень и очень похоже на правду.

На заключительном этапе отмечаем на чертеже точку . По условию не требовалось ничего чертить, но в большинстве задач мы волей-неволей вынуждены изобразить фигуру. Зато есть безусловный плюс – визуальная и довольно эффективная проверка результата.

Ответ :

Следующие два примера для самостоятельного решения.

Пример 2

Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями

Кстати, если вы представляете, как расположена парабола и увидели точки, в которых она пересекает ось , то здесь и на самом деле можно обойтись без чертежа.

И посложнее:

Пример 3

Найти центр тяжести однородной плоской фигуры, ограниченной линиями

В случае затруднений с построением графиков, изучите (повторите) урок о параболах и/или Пример №11 статьи Двойные интегралы для чайников .

Примерные образцы решений в конце урока.

Кроме того, десяток-другой похожих примеров можно найти в соответствующем архиве на странице Готовые решения по высшей математике .

Ну а я не могу не порадовать любителей высшей математики, которые часто просят меня разбирать и трудные задачки:

Пример 4

Найти центр тяжести однородной плоской фигуры, ограниченной линиями . Фигуру и её центр тяжести изобразить на чертеже.

Решение : условие данной задачи уже категорично требует выполнения чертежа. А ведь требование не настолько и формально! – эту фигуру способен представить в уме даже человек со средним уровнем подготовки:

Прямая рассекает круг на 2 части, и дополнительная оговорка (см. линейные неравенства ) указывает на то, что речь идёт именно о маленьком заштрихованном кусочке.

Фигура симметрична относительно прямой (изображена пунктиром), поэтому центр тяжести должен лежать на данной линии. И, очевидно, что его координаты равны по модулю . Отличный ориентир, практически исключающий ошибочный ответ!

Теперь плохая новость =) На горизонте маячит малоприятный интеграл от корня, который мы подробно разобрали в Примере №4 урока Эффективные методы решения интегралов . И кто его знает, что там нарисуется ещё. Казалось бы, ввиду наличия окружности выгодно , однако не всё так просто. Уравнение прямой преобразуется к виду и интегралы тоже получатся не сахарные (хотя фанаты тригонометрических интегралов оценят). В этой связи осмотрительнее остановиться на декартовых координатах.

Порядок обхода фигуры:

1) Вычислим площадь фигуры:

Первый интеграл рациональнее взять подведением под знак дифференциала :

А во втором интеграле проведём стандартную замену :

Вычислим новые пределы интегрирования:

2) Найдём .

Здесь во 2-м интеграле опять был использован метод подведения функции под знак дифференциала . Отработайте и возьмите на вооружение эти оптимальные (по моему мнению) приёмы решения типовых интегралов.

После непростых и длительных вычислений вновь обращаем свой взор на чертёж (помним, что точки мы пока не знаем! ) и получаем глубокое моральное удовлетворение от найденного значения .

3) Исходя из проведённого ранее анализа, осталось убедиться, что .

Отлично:

Изобразим точку на чертеже. В соответствии с формулировкой условия запишем её как окончательный ответ :

Похожее задание для самостоятельного решения:

Пример 5

Найти центр тяжести однородной плоской фигуры, ограниченной линиями . Выполнить чертёж.

Эта задача интереса тем, что в ней задана фигура достаточно малых размеров, и если где-нибудь допустить ошибку, то высока вероятность вообще «не попасть» в область. Что, безусловно, хорошо с точки зрения контроля решения.

Примерный образец оформления в конце урока.

Иногда бывает целесообразен переход к полярным координатам в двойных интегралах . Это зависит от фигуры. Искал-искал у себя удачный пример, но не нашёл, поэтому продемонстрирую ход решения на 1-й демо-задаче указанного выше урока:


Напоминаю, что в том примере мы перешли к полярным координатам , выяснили порядок обхода области и вычислили её площадь

Давайте найдём центр тяжести данной фигуры. Схема та же: . Значение просматривается прямо из чертежа, а «иксовая» координата должна быть смещена чуть ближе к оси ординат, поскольку там располагается более массивная часть полукруга.

В интегралах используем стандартные формулы перехода:

Правдоподобно, скорее всего, не ошиблись.

Лекция 4. Центр тяжести.

В данной лекции рассматриваются следующие вопросы

1. Центр тяжести твердого тела.

2. Координаты центров тяжести неоднородных тел.

3. Координаты центров тяжести однородных тел.

4. Способы определения координат центров тяжести.

5. Центры тяжести некоторых однородных тел.

Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов».

Приведение параллельных сил.

После того как было рассмотрено приведение к центру плоской системы и произвольной пространственной системы сил, мы опять возвращаемся к рассмотрению частного случая системы параллельных сил.

Приведение двух параллельных сил.

В ходе рассмотрения такой системы сил возможны три следующих случая приведения.

1. Система двух коллинеарных сил. Рассмотрим систему двух параллельных и направленных в одну сторону сил P и Q , приложенных в точках А и В . Будем считать, что силы перпендикулярны к этому отрезку (рис.1,а ).

С , принадлежащую отрезку АВ и удовлетворяющую условию:

АС /СВ = Q /P .(1)

Главный вектор системы R C = P + Q по модулюравен сумме этих сил:R C = P + Q .

С с учетом (1) равен нулю: M C = P ∙ АС - Q ∙ СВ = 0.

Таким образом, в результате приведения мы получили: R C ≠ 0, M C = 0. Это означает, что главный вектор эквивалентен равнодействующей, проходящей через центр приведения, то есть:

Равнодействующая коллинеарных сил равна по модулю их сумме, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внутренним образом.

Отметим, что положение точки С не изменится, если силы Р и Q повернуть на угол α . Точка С , обладающая таким свойством называется центром параллельных сил .

2. Система двух антиколлинеарных и не равных по модулю сил. Пусть силы P и Q , приложенные в точках А и В , параллельны, направлены в противоположные стороны и по модулю не равны (рис.1,б ).

Выберем в качестве центра приведения точку С , удовлетворяющую по-прежнему соотношению (1) и лежащую на той же прямой, но за пределами отрезка АВ .

Главный вектор этой системыR C = P + Q по модулю теперь будет равен разности модулей векторов:R C = Q - P .

Главный момент относительно центра С по-прежнему равен нулю: M C = P ∙ АС - Q ∙ СВ = 0, поэтому

Равнодействующая антиколлинеарных и не равных по модулю сил равна их разности, направлена в сторону большей силы, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внешнимобразом.

Рис.1

3. Система двух антиколлинеарных и равных по модулю сил. Возьмем за исходный предыдущий случай приведения. Зафиксируем силу Р , а силу Q устремим по модулю к силеР .

Тогда при Q → Р в формуле (1) отношение АС /СВ → 1. Это означает, чтоАС → СВ , то есть расстояние АС →∞ .

При этом модуль главного вектора R C → 0, а модуль главного момента не зависит от положения центра приведения и остается равным первоначальному значению:

M C = P ∙ АС - Q ∙ СВ = P ∙ ( АС - СВ ) = P ∙ А B .

Итак, в пределе мы получили систему сил, для которой R C = 0, M C ≠ 0, а центр приведения удален в бесконечность, которую нельзя заменить равнодействующей. В этой системе нетрудно узнать пару сил, поэтому пара сил равнодействующей не имеет .

Центр системыпараллельных сил.

Рассмотрим систему n сил P i , приложенных в точках A i (x i , y i , z i )и параллельных оси Ov c ортом l (рис.2).

Если заранее исключить случай системы, эквивалентной паре сил, нетрудно на основании предыдущего параграфа доказать существование ее равнодействующей R .

Определим координаты центра C (x c , y c , z c ) параллельных сил, то есть координаты точки приложения равнодействующейэтой системы.

Воспользуемся с этой целью теоремой Вариньона, на основании которой:

M 0 (R ) = Σ M 0 (P i ).

Рис.2

Вектор-момент силы можно представить в виде векторного произведения, поэтому:

М 0 (R ) = r c × R = Σ М 0i (P i ) = Σ (r i × P i ).

Учитывая, что R = R v ∙ l , а P i = P vi ∙ l и воспользовавшись свойствами векторного произведения, получим:

r c × R v ∙ l = Σ (r i × P vi ∙ l ),

r c ∙ R v × l = Σ (r i ∙ P vi × l ) = Σ (r i ∙ P vi ) × l ,

или:

[ r c R v - Σ (r i P vi )] × l = 0.

Последнее выражение справедливо только в том случае, если выражение в квадратных скобках равно нулю. Поэтому, опуская индекс v и учитывая, что равнодействующая R = Σ P i , отсюда получим:

r c = (Σ P i r i )/(Σ P i ).

Проектируя последнее векторное равенство на оси координат, получим искомое выражение координат центра параллельных сил :

x c = (Σ P i x i )/(Σ P i );

y c = (Σ P i y i )/(Σ P i );(2)

z c = (Σ P i z i )/(Σ P i ).

Центр тяжести тел.

Координаты центров тяжести однородного тела.

Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.

Если разбить тело на элементарные части объемом ∆ V i , то на каждую его часть будет действовать сила притяжения ∆ P i , направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.3), и к ней применимы все выводы предыдущей главы.

Рис.3

Определение . Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.

Напомним, что удельным весом элементарной части тела называется отношение ее веса ∆ P i к объему ∆ V i : γ i = ∆ P i / ∆ V i . Для однородного тела эта величина является постоянной: γ i = γ = P / V .

Подставляя в (2) ∆ P i = γ i ∙∆ V i вместо P i , учитывая последнее замечание и сокращая числитель и знаменатель на g , получим выражения координат центра тяжести однородного тела :

x c = (Σ ∆ V i ∙ x i )/(Σ ∆ V i );

y c = (Σ ∆ V i ∙ y i )/(Σ ∆ V i );(3)

z c = (Σ ∆ V i ∙ z i )/(Σ ∆ V i ).

При определении центра тяжести полезны несколько теорем.

1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоско­сти.

Если оси х и у расположить в этой плоскости симметрии, то для каждой точки с координатами . И координата по (3), бу­дет равна нулю, т.к. в сумме все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.

2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Действительно, в этом случае, если ось z провести по оси симмет­рии, для каждой точки с координатами можно отыскать точку с координатами и координаты и , вычисленные по фор­мулам (3), окажутся равными нулю.

Аналогично доказывается и третья теорема.

3) Если однородное тело имеет центр симметрии, то центр тя­жести тела находится в этой точке.

И ещё несколько замечаний.

Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (3) P i – определять как вес соответствующей части и – как координаты её центра тяжести.

Второе. Если тело однородное, то вес отдельной части его , где - удельный вес материала, из которого сделано тело, а V i - объём этой части тела. И формулы (3) примут более удобный вид. Например,

И аналогично, где - объём всего тела.

Третье замечание. Пусть тело имеет вид тонкой пластинки площадью F и толщиной t , лежащей в плоскости Oxy . Подставляя в (3) ∆ V i = t ∙ ∆ F i , получим координаты центра тяжести однородной пластинки :

x c = (Σ ∆ F i ∙ x i ) / (Σ ∆ F i );

y c = (Σ ∆ F i ∙ y i ) / (Σ ∆ F i ).

z c = (Σ ∆ F i ∙ z i ) / (Σ ∆ F i ).

где – координаты центра тяжести отдельных пластин; – общая площадь тела.

Четвёртое замечание. Для тела в виде тонкого криволинейного стержня длиной L с площадью поперечного сечения a элементарный объем ∆ V i = a ∙∆ L i , поэтому координаты центра тяжести тонкого криволинейного стержня будут равны:

x c = (Σ ∆ L i ∙ x i )/(Σ ∆ L i );

y c = (Σ ∆ L i ∙ y i )/(Σ ∆ L i );(4)

z c = (Σ ∆ L i ∙ z i )/(Σ ∆ L i ).

где – координаты центра тяжести i -го участка; .

Отметим, что согласно определению центр тя­жести - это точка геометрическая; она может лежать и вне преде­лов данного тела (например, для кольца).

Примечание.

В этом разделе курса мы не делаем разницы между силой притяжения, силой тяжести и весом тела. В действительности сила тяжести представляет собой разность между силой притяжения Земли и центробежной силой, вызванной ее вращением.

Координаты центров тяжести неоднородных тел.

Координаты центра тяжести неоднородного твердого тела (рис.4) в выбранной системе отсчета определяются следующим образом:

Рис.4

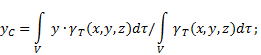
где - вес единицы объема тела (удельный вес)

-вес всего тела.

неоднородную поверхность (рис.5), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

Рис.5

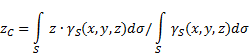
где - вес единицыплощади тела,

-вес всего тела.

Если твердое тело представляет собой неоднородную линию (рис.6), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

Рис.6

где - вес единицыдлины тела,

Вес всего тела.

Способы определения координат центра тяжести.

Исходя из полученных выше общих формул,можно указать конкретные способы определения координат центров тяжести тел .

1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.7), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Рис.7

2. Разбиение. Тело разбивается на конечное число частей (рис.8), для каждой из которых положение центра тяжести и площадь известны.

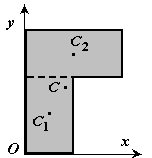
Рис.8

S =S 1 +S 2 .

3. Метод отрицательных площадей. Частный случай способа разбиения (рис.9). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки(без выреза) с площадью S 1 и площади вырезанной части S 2 .

Рис.9

S = S 1 - S 2 .

4. Метод группировки. Является хорошим дополнением двух последних методов. После разбиения фигуры на составные элементы часть их бывает удобно объединить вновь, чтобы затем упростить решение путем учета симметрии этой группы.

Центры тяжести некоторых одно­родных тел.

1) Центр тяжести дуги окруж­ности. Рассмотрим дугу АВ радиуса R с центральным углом . В силу сим­метрии центр тяжести этой дуги лежит на оси Ox (рис. 10).

Рис.10

Найдем координату по формуле . Для этого выделим на дуге АВ элемент ММ ’ длиною , положение которого определяется углом . Координата х элемента ММ’ будет . Подставляя эти значения х и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:

где L - длина дуги АВ , равная .

Отсюда окончательно нахо­дим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О , равном

где угол измеряется в радианах.

2) Центр тяжести площади тре­угольника. Рассмотрим треугольник, лежащий в плоскости Oxy , координаты вершин которого известны: A i (x i ,y i ), (i = 1,2,3). Разбивая треугольник на узкие полоски, параллельные стороне А 1 А 2 , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А 3 М 3 (рис.11) .

Рис.11

Разбивая треугольник на полоски, параллельные стороне А 2 А 3 , можно убедиться, что он должен лежать на медиане А 1 М 1 . Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан , которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.

В частности, для медианы А 1 М 1 получим, учитывая, что координаты точки М 1 - это среднее арифметическое координат вершин А 2 иА 3 :

x c = x 1 + (2/3) ∙ (x М 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.

Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:

x c =(1/3) Σ x i ; y c =(1/3) Σ y i .

3) Центр тяжести площади кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2 α , расположенный симметрично относительно оси Ox (рис.12) .

Очевидно, что y c = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле:

Рис.12

Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом d φ . С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным R × d φ и высотой R . Площадь такого треугольника dF =(1/2)R 2 ∙ d φ , а его центр тяжести находится на расстоянии 2/3R от вершины, поэтому в (5) положим x = (2/3)R ∙ cosφ . Подставляя в (5) F = α R 2 , получим:

С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга .

Подставляя в (2) α = π /2, получим: x c = (4 R )/(3 π ) ≅ 0,4 R .

Пример 1. Определим центр тяжести однородного тела, изображён­ного на рис. 13.

Рис.13

Решение. Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:

Объёмы их:

Поэтому координаты центра тяжести тела

Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.14).

Рис.14

Решение. Координаты центров тяжести:

0.

Площади:

Поэтому:

Пример 3. У квадратного листа см вырезано квадратное отверстие см (рис.15). Найдем центр тяжести листа. Пример 4. Найти положение центра тяжести пластинки, представленной на рис. 16. Размеры даны в сантиметрах.

Рис.16

Решение. Разделим пластинку на фигуры (рис. 17), центры тяжести которых известны.

Площади этих фигур и координаты их центров тяжести:

1) прямоугольник со сторонами 30 и 40 см, S 1 =30 ∙ 40=1200 см 2 ; х 1 =15 см; у 1 =20 см.

2) прямоугольный треугольник с основанием 50 см и высотой 40 см; S 2 =0,5 ∙ 50 ∙ 40= 1000 см 2 ; х 2 =30+50/3=46,7 см;у 2 = 40/3 =13,3 см;

3) половина круга окружности радиуса r = 20 см; S 3 =0,5 ∙π∙ 20 2 =628 см 2 ; х 3 =4 R /3 π =8,5 см; у

Решение. Напомним, что в физике плотность тела ρ и его удельный вес g связаны соотношением: γ = ρ g , где g - ускорение свободного падения. Чтобы найти массу такого однородного тела, нужно плотность умножить на его объем.

Рис.19

Термин «линейная» или «погонная» плотность означает, что для определения массы стержня фермы нужно погонную плотность умножить на длину этого стержня.

Для решения задачи можно воспользоваться методом разбиения. Представив заданную ферму в виде суммы 6 отдельных стержней, получим:

где L i длина i -го стержня фермы, а x i , y i - координаты его центра тяжести.

Решение этой задачи можно упростить, если сгруппировать 5 последних стержней фермы. Нетрудно видеть, что они образуют фигуру, имеющую центр симметрии, расположенный посредине четвертого стержня, где и находится центр тяжести этой группы стержней.

Таким образом, заданную ферму можно представить комбинацией всего двух групп стержней.

Первая группа состоит из первого стержня,для нее L 1 = 4 м, x 1 = 0 м, y 1 = 2 м. Вторая группа стержней состоит из пяти стержней, для нее L 2 = 20 м, x 2 = 3 м, y 2 = 2 м.

Координаты центра тяжести фермы находим по формуле:

x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 м;

y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 м.

Отметим, что центр С лежит на прямой, соединяющей С 1 и С 2 и делит отрезок С 1 С 2 в отношении: С 1 С /СС 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.

Вопросы для самопроверки

- Что называется центром параллельных сил?

- Как определяются координаты центра параллельных сил?

- Как определить центр параллельных сил, равнодействующая которых равна нулю?

- Каким свойством обладает центр параллельных сил?

- По каким формулам вычисляются координаты центра параллельных сил?

- Что называется центром тяжести тела?

- Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?

- Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?

- Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?

- Что называют статическим моментом площади?

- Приведите пример тела, центр тяжести которого расположен вне тела.

- Как используются свойства симметрии при определении центров тяжести тел?

- В чем состоит сущность способа отрицательных весов?

- Где расположен центр тяжести дуги окружности?

- Каким графическим построением можно найти центр тяжести треугольника?

- Запишите формулу, определяющую центр тяжести кругового сектора.

- Используя формулы, определяющие центры тяжести треугольника и кругового сектора, выведите аналогичную формулу для кругового сегмента.

- По каким формулам вычисляются координаты центров тяжести однородных тел, плоских фигур и линий?

- Что называется статическим моментом площади плоской фигуры относительно оси, как он вычисляется и какую размерность имеет?

- Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?

- Какими вспомогательными теоремами пользуются при определении положения центра тяжести?

Прямоугольник. Так как прямоугольник имеет две оси симметрии, то его центр тяжести находится на пересечении осей симметрии, т.е. в точке пересечения диагоналей прямоугольника.

Треугольник. Центр тяжести лежит в точке пересечения его медиан. Из геометрии известно, что медианы треугольника пересекаются в одной точке и делятся в отношении 1:2 от основания.

Круг. Так как круг имеет две оси симметрии, то его центр тяжести находится на пересечении осей симметрии.

Полукруг. Полукруг имеет одну ось симметрии, то центр тяжести лежит на этой оси. Другая координата центра тяжести вычисляется по формуле: .

Многие конструктивные элементы изготавливают из стандартного проката – уголков, двутавров, швеллеров и других. Все размеры, а так же геометрические характеристики прокатных профилей это табличные данные, которые можно найти в справочной литературе в таблицах нормального сортамента (ГОСТ 8239-89, ГОСТ 8240-89).

Пример 1. Определить положение центра тяжести фигуры, представленной на рисунке.

Решение:

Выбираем оси координат, так чтобы ось Ох прошла по крайнему нижнему габаритному размеру, а ось Оу – по крайнему левому габаритному размеру.

Разбиваем сложную фигуру на минимальное количество простых фигур:

прямоугольник 20х10;

треугольник 15х10;

круг R=3 см.

Вычисляем площадь каждой простой фигуры, её координаты центра тяжести. Результаты вычислений заносим в таблицу

№ фигуры	Площадь фигуры А,	Координаты центра тяжести

Ответ: С(14,5; 4,5)

Пример 2 . Определить координаты центра тяжести составного сечения, состоящего из листа и прокатных профилей.

Решение.

Выбираем оси координат, так как показано на рисунке.

Обозначим фигуры номерами и выпишем из таблицы необходимые данные:

№ фигуры	Площадь фигуры А,	Координаты центра тяжести

Вычисляем координаты центра тяжести фигуры по формулам:

Ответ: С(0; 10)

Лабораторная работа №1 «Определение центра тяжести составных плоских фигур»

Цель: Определить центр тяжести заданной плоской сложной фигуры опытным и аналитическим способами и сравнить их результаты.

Порядок выполнения работы

Начертить в тетрадях свою плоскую фигуру по размерам, с указанием осей координат.

Определить центр тяжести аналитическим способом.

1. Разбить фигуру на минимальное количество фигур, центры тяжести которых, мы знаем, как определить.

   Указать номера площадей и координаты центра тяжести каждой фигуры.

   Вычислить координаты центра тяжести каждой фигуры.

   Вычислить площадь каждой фигуры.

   Вычислить координаты центра тяжести всей фигуры по формулам (положение центра тяжести нанести на чертеж фигуры):

Установка для опытного определения координат центра тяжести способом подвешивания состоит из вертикальной стойки 1 (см. рис.), к которой прикреплена игла 2 . Плоская фигура 3 изготовлена из картона, в котором легко проколоть отверстие. Отверстия А и В прокалываются в произвольно расположенных точках (лучше на наиболее удаленном расстоянии друг от друга). Плоская фигура подвешивается на иглу сначала в точке А , а потом в точке В . При помощи отвеса 4 , закрепленного на той же игле, на фигуре прочерчивают карандашом вертикальную линию, соответствующую нити отвеса. Центр тяжести С фигуры будет находиться в точке пересечения вертикальных линий, нанесенных при подвешивании фигуры в точках А и В .

Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.

Центр тяжести стержня находится на середине высоты. При решении задач используются следующие методы:

1. метод симметрии: центр тяжести симметричных фигур нахо­дится на оси симметрии;

2. метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко опреде­лить;

3. метод отрицательных площадей: полости (отверстия) рас­сматриваются как часть сечения с отрицательной площадью.

Примеры решения задач

Пример1. Определить положение центра тяжести фигуры, представленной на рис. 8.4.

Решение

Разбиваем фигуру на три части:

Аналогично определяется у С = 4,5 см.

Пример 2. Найти положение центра тяжести симметричной стержневой фермы ADBE (рис. 116), размеры которой таковы: АВ = 6м, DE = 3 м и EF = 1 м.

Решение

Так как ферма симметричная, то ее центр тяжести лежит на оси симметрии DF. При выбранной (рис. 116) системе коор­динатных осей абсцисса центра тяжести фермы

Неизвестной, следовательно, является лишь ордината у С центра тя­жести фермы. Для ее определения разбиваем ферму на отдельные части (стержни). Длины их определяются из соответствующих треугольников.

Из ΔAEF имеем

Из ΔADF имеем

Центр тяжести каждого стержня лежит в его середине, координаты этих центров легко определяются из чертежа (рис. 116).

Найденные длины и ординаты центров тяжести отдельных частей фермы заносим в таблицу и по формуле

определяем ординату у с центра тяжести данной плоской фермы.

Следовательно, центр тяжести С всей фермы лежит на оси DF симметрии фермы на расстоянии 1,59 м от точки F.

Пример 3. Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).

Примечание. Часто рамы сваривают из разных профилей, создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.

Для стандартных прокатных профилей собственные геометри­ческие характеристики известны. Они приводятся в соответствую­щих стандартах.

Решение

1. Обозначим фигуры номерами и выпишем из таблиц необхо­димые данные:

1 - швеллер № 10 (ГОСТ 8240-89); высота h = 100 мм; ширина полки b = 46 мм; площадь сечения А 1 = 10,9 см 2 ;

2 - двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина полки 81 мм; площадь сечения А 2 - 20,2 см 2 ;

3 - лист 5x100; толщина 5 мм; ширина 100мм; площадь сечения A 3 = 0,5 10 = 5 см 2 .

2. Координаты центров тяжести каждой фигуры можно опреде­лить по чертежу.

Составное сечение симметрично, поэтому центр тяжести нахо­дится на оси симметрии и координата х С = 0.

3. Определение центра тяжести составного сечения:

Пример 4. Определить координаты центра тяжести сечения, по­казанного на рис. 8, а. Сечение состоит из двух уголков 56x4 и швеллера № 18. Выполнить проверку правильности определения положения центра тяжести. Указать его положение на сечении.

Решение

1. : два уголка 56 х 4 и швеллер № 18. Обозначим их 1, 2, 3 (см. рис. 8, а).

2. Укажем центры тяжести каждого профиля, используя табл. 1 и 4 прил. I, и обозначим их С 1 , С 2 , С 3 .

3. Выберем систему координатных осей. Ось у совместим с осью симметрии, а ось х проведем через центры тяжести уголков.

4. Определим координаты центра тяжести всего сечения. Так как ось у совпадает с осью симметрии, то она проходит через центр тяжести сечения, поэтому х с = 0. Координату у с опреде­лим по формуле

Пользуясь таблицами приложения, определим площади каждого профиля и координаты центров тяжести:

Координаты у 1 и у 2 равны нулю, так как ось х проходит через центры тяжести уголков. Подставим полученные значения в формулу для определения у с :

5. Укажем центр тяжести сечения на рис. 8, а и обозначим его буквой С. Покажем расстояние у С = 2,43 см от оси х до точ­ки С.

Поскольку уголки симметрично расположены, имеют одина­ковую площадь и координаты, то А 1 = А 2 , у 1 = у 2 . Поэтому фор­мула для определения у С может быть упрощена:

6. Выполним проверку. Для этого ось х проведем по нижнему краю полки уголка (рис. 8, б). Ось у оставим, как в первом ре­шении. Формулы для определения х С и у С не изменяются:

Площади профилей останутся такими же, а координаты центров тяжестей уголков и швеллера изменятся. Выпишем их:

Находим координату центра тяжести:

По найденным координатам х с и у с наносим на рисунок точ­ку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Проверим это. Разница между координатами у с, найденными при первом и втором решении, составляет: 6,51 - 2,43 = 4,08 см.

Это равно расстоянию между осями х при первом и втором решении: 5,6 - 1,52 = 4,08 см.

Ответ: у с = 2,43 см, если ось х проходит через центры тяже­сти уголков, или у с = 6,51 см, если ось х проходит по нижнему краю полки уголка.

Пример 5. Определить координаты центра тяжести сечения, изображенного на рис. 9, а. Сечение состоит из двутавра № 24 и швеллера №.24а. Показать положение центра тяжести на сече­нии.

Решение

1. Разобьем сечение на профили проката : двутавр и швеллер. Обозначим их цифрами 1 и 2.

3. Укажем центры тяжести каждого профиля С 1 и С 2 , ис­пользуя таблицы приложений.

4. Выберем систему осей координат. Ось х совместим с осью симметрии, а ось у проведем через центр тяжести двутавра.

5. Определим координаты центра тяжести сечения. Координа­та у с = 0, так как ось х совпадает с осью симметрии. Координату х с определим по формуле

По табл. 3 и 4 прил. I и схеме сечения определим

Подставим числовые значения в формулу и получим

5. Нанесем точку С (центр тяжести сечения) по найденным значениям х с и у с (см. рис. 9, а).

Проверку решения необходимо выполнить самостоятельно при положении осей, как показано на рис. 9, б. В результате ре­шения получим х с = 11,86 см. Разница между значениями х с при первом и втором решении равна 11,86 - 6,11 = 5,75 см, что равно расстоянию между осями у при тех же решениях b дв /2 = 5,75 см.

Ответ: х с = 6,11 см, если ось у проходит через центр тяжести двутавра; х с = 11,86 см, если ось у проходит через левые крайние точки двутавра.

Пример 6. Железнодорожный кран опирается на рельсы, расстояние меж­ду которыми АВ = 1,5м (рис. 1.102). Сила тяжести тележки крана G r = 30 кН, центр тяжести тележки находится в точке С, лежащей на линии KL пересечения плоскости симметрии тележки с плоскостью рисунка. Сила тяжести лебедки крана Q л = 10 кН приложена в точке D. Сила тяжести противовеса G„=20 кН приложена в точке Е. Сила тяжести стрелы G c = 5 кН приложена в точке Н. Вылет крана относительно линии KL равен 2 м. Определить коэффициент устойчивости крана в ненагруженном состоянии и какой груз F можно поднять этим краном при условии, что коэффициент устойчивости должен быть не менее двух.

Решение

1. В ненагруженном состоянии у крана возникает опасность опро­кидывания при повороте вокруг рельса А. Следовательно, относительно точки А момент устойчивости

2. Опрокидывающий момент относительно точки А создается силой тяжести противове­са, т. е.

3. Отсюда коэффициент устойчивости крана в ненагруженном состоянии

4. При нагрузке стрелы крана грузом F возникает опасность опрокидывания крана с поворотом около рельса В. Следовательно, от­носительно точки В момент устойчивости

5. Опрокидывающий момент относитель­но рельса В

6. По условию задачи эксплуатация крана разрешается при коэффициенте устойчивости k B ≥ 2 , т. е.

Контрольные вопросы и задания

1. Почему силы притяжения к Земле, действующие на точки тела, можно принять за систему параллельных сил?

2. Запишите формулы для определения положения центра тя­жести неоднородных и однородных тел, формулы для определения положения центра тяжести плоских сечений.

3. Повторите формулы для определения положения центра тя­жести простых геометрических фигур: прямоугольника, треугольни­ка, трапеции и половины круга.

4.
Что называют статическим моментом площади?

5. Вычислите статический момент данной фигуры относительно оси Ox. h = 30 см; b = 120 см; с = 10 см (рис. 8.6).

6. Определите координаты центра тяжести заштрихованной фи­гуры (рис. 8.7). Размеры даны в мм.

7. Определите координату у фигуры 1 составного сечения (рис. 8.8).

При решении воспользоваться справочными данными таблиц ГОСТ «Сталь горячекатанная» (см. Приложение 1).

Для создания поделок, головоломок да и просто в домашних делах, иногда возникает ситуация когда необходимо рассчитать центр тяжести какой либо фигуры. И если для простейших фигур, формулы расчета центра тяжести известны, например для круга центр тяжести совпадает с центром окружности, то более сложные фигуры, а тем более фигуры состоящие из ломаных линий, вручную посчитать очень сложно.

Что же такое центр тяжести? Это такая точка на фигуре, поднимая за которую, фигура остается в таком же положении как она лежала например на столе. Это дилетанское конечно же объяснение, кроме этого мы говорим о плоских фигурах. Более правильное такое: Центром тяжести механической системы называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю .

Калькулятор рассчитвает центр тяжести любой плоской однородной по составу фигуры, состоящей из ломаных линий.

Что же Вам, как пользователю необходимо знать? Необходимы координаты точек вершин такого многоугольника.

Как определить центр тяжести?

Если на точки М1(x1,y1,z1) и М2(x2,y2,z2 ) действуют паралельные силы то точка М приложения равнодействующей этих сил делит отрезок М1М2 обратно пропорционально этим силам

Поэтому координаты точки М будут

если речь идет о воздействии трех действующих сил то формулы аналогичные и высчитываются как арифметическое средневзвешенное

таким же способом рассчитываются если в точках приложения сил не три, а четыре или пять или десять например.

Если принять что силой действующий на точки будет сила тяжести, а масса точек будет одинакова, то после сокращений одинаковых значений, наша формула для трех точек будет следующей

Здесь положение центра тяжести зависит только от положения точек. Точка () называется геометрическим центром тяжести этих точек

Если фигура симметрична - то центр тяжести совпадает с геометрическим центром фигуры. Это касается таких например фигур как квадрат, круг, правильный многоугольник, равносторонний треугольник и другие подобные объекты.

И еще, немного теории, которая поможет рассчитать центр тяжести сложных фигур.

Положение центра тяжести чистемы точечных масс не изменится, если любую частичную группу точечных масс системы заменить одной точечной массой, расположенной в центре тяжести этой группы и имеющей в качестве массы сумму масс точек этой группы.

РАСЧЕТ ЦЕНТРА ТЯЖЕСТИ ТРЕУГОЛЬНИКА ПО КООРДИНАТАМ

Рассчитаем центр тяжести треугольной пластины, произвольной формы, одинаковой толщины.

Из какого материала мы будем делать, из стали, бумаги или платика не столь важно.

Центр тяжести трегольника является одной из семи замечательных точек, и определяется как точка пересечения медиан сторон этого треугольника.

Если же нам известны только координаты треугольника, например, мы его вырезали из тетрадки в клеточку, то координаты точки тяжести, будут определяться так

Не пытайтесь аппроксимировать эту формулу и подумать что центр трапеции будет вычисляться аналогично например по таким формулам

Это неверно, вернее неверно в случае когда масса распределена в плоскости между этими точками (например пластины).

Если же речь идет о точечных массах расположенных в этих координатах, то формула центра масс, будет правильной.

РАСЧЕТ ЦЕНТРА ТЯЖЕСТИ трапеции ПО КООРДИНАТАМ

Как же тогда рассчитывать центр тяжести трапеции?

Умные люди нашли формулу расчета точки, но в ней исходные данные представлены в виде длин сторон трапеции.

Вот эта формула.

Она не удобна, когда нам известны только координаты трапеции. Но мы воспользуемся способом разбиения трапеции два треугольника, где для каждого из них находим центр тяжести, а потом рассчитывая уже для двух точек(центров), находим окончательное решение.

Для каждого треугольника центр будет рассчитыватся по известной формуле

Но вот, когда мы будем рассчитывать окончательную точку, надо учитывать что мы, "стягивая" в центр тяжести каждый треугольник, стягиваем и всю массу поверхности которая лежала между этими координатами.

Так как между площадью фигуры (при одинаковой толщине) и массой связь линейная, то легко предположить что окончательный расчет будет не таким